Non-Lifting Flow over a Circular Cylinder

It is seen earlier that flow over a semi-infinite body can be simulated by combination of a uniform flow with a source and flow over an oval-shaped body can be constructed by superimposing a uniform flow and a source-sink pair. A circular cylinder is one of the basic geometrical shapes and the flow passing over it can be simulated by combination of a uniform flow and doublet. When the distance between source-sink pair approaches zero, the shape Rankine oval becomes more blunt and approaches a circular shape.

Consider the superposition of a uniform flow of velocity and a doublet of strength as shown in Fig. 3.7.1. The direction of the doublet is upstream, facing into uniform flow.

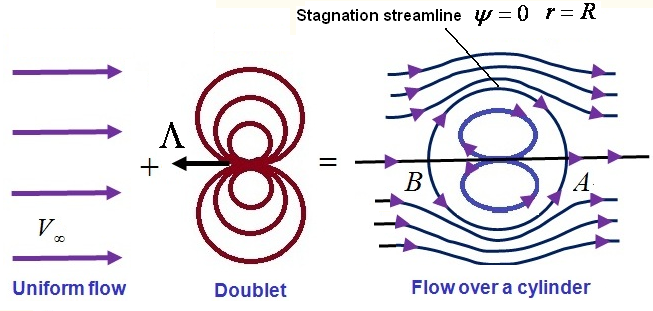
Fig. 3.7.1: Superposition of a uniform flow and doublet.

The stream function for the combined flow is,

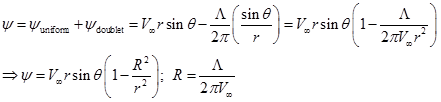(3.7.1)

The velocity field is obtained as,

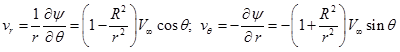(3.7.2)

In order to locate the stagnation point, assign the velocity components in Eq. (3.7.2) to zero value and simultaneously solve for . There are two stagnation points, located at and denoted by points A and B, respectively. The equation of streamlines that passes through the stagnation points A and B, is given by the following expression;

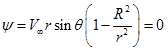(3.7.3)