Irrotational Flow
In Eq.(3.2.11) , if 
is zero, then the rotation and vorticity are zero. The flow fields for which the above condition is applicable is known as irrotational flow. The condition of irrotationality imposes specific relationship among the velocity gradients which is applicable for inviscid flow. If the rotations about the respective orthogonal axes are to be zero, then, one can write Eq. (3.2.11) as,
 |
(3.2.12) |
A general flow field would never satisfy all the above conditions. However, a uniform flow field defined in a fashion, for which 
, is certainly an example of an irrotational flow because there are no velocity gradients. A fluid flow which is initially irrotational may become rotational if viscous effects caused by solid boundaries, entropy gradients and density gradients become significant.
Circulation
It is defined as the line integral of the tangential velocity component about any closed curve fixed in the flow i.e.
 |
(3.2.13) |
where, 
is an elemental vector tangent to the curve and with length ds with counterclockwise path of integration considered as positive. For the closed curve path OACB as shown in Fig. 3.2.4-a, we can develop the relationship between circulation and vorticity as follows;
 |
|
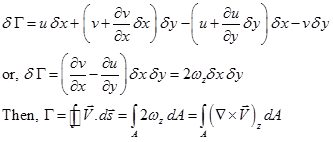Hence, circulation around a closed contour is equal to total vorticity enclosed within it. It is known as Stokes theorem in two dimensions.