Angular Motion and Deformation
The variations of velocity in the direction of velocity is represented by the partial derivatives 
, which causes linear deformation in the sense that shape of the fluid element does not change. However, cross variations of derivatives such as 
will cause the fluid element to rotate. These motions lead to angular deformation which generally changes the shape of the element.
Fig. 3.2.4: Angular deformation of a fluid element.
Let us consider the angular motion in x-y plane in which the initial shape is given by OACB , as shown in Fig. 3.2.4-a. The velocity variations cause the rotation and angular deformation so that the new positions become OA' and OB ' after a time interval 
. Then the angles AOA' and BOB' are given by 
, respectively as shown in Fig. 3.2.4-b. Thus, the angular velocities of line OA and OB are,
 |
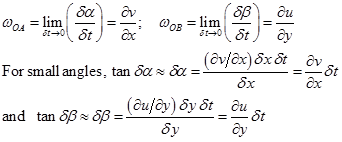(3.2.5) |
When, both 
are positive, then both 
will be in counterclockwise direction. Now, the rotation of the fluid element about z-direction (i.e x-y plane) 
can be defined as the average of 
. If counterclockwise rotation is considered as positive, then
 |
(3.2.6) |
In a similar manner, the rotation of the fluid element about x and y axes are denoted as 
, respectively.
 |
(3.2.7) |
These three components can be combined to define the rotation vector 
in the form as,
 |
|
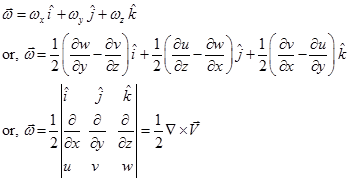