It is observed from Eq.(3.2.6) that the fluid element will rotate about z- axis, as an undeformed block, only when, . Otherwise it will be associated with angular deformation which is characterized by shear strain rate. When the fluid element undergoes shear deformation (Fig. 3.2.2-b), the average shear strain rates expressed in different cartesian planes as,

(3.2.9)

Strain rate as a whole constitute a symmetric second order tensor i.e.

(3.2.10)

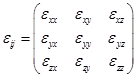Vorticity

In a flow field, vorticity is related to fluid particle velocity which is defined as twice of rotation vector i.e.

(3.2.11)

Thus, the curl of the velocity vector is equal to the vorticity. It leads to two important definitions:

• • If 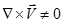at every point in the flow, the flow is called as rotational. It implies that the fluid elements have a finite angular velocity.

• If at every point in the flow, the flow is called as irrotational. It implies that the fluid elements have no angular velocity rather the motion is purely translational.