·        

Linear Motion and Deformation

Translation is the simplest type of fluid motion in which all the points in the fluid element have same velocity. As shown in Fig. 3.2.3-a, the particle located as point O will move to O' during a small time interval . When there is a presence of velocity gradient, the element will tend to deform as it moves. Now, consider the effect of single velocity gradient on a small cube having sides and volume . As shown in Fig. 3.2.3-b, the x -component of velocity of O and B is u. Then, x- component of velocity of points A and C would be, , which causes stretching of AA' by an amount as shown in Fig.3.2.3-c. So, there is a change in the volume element

 

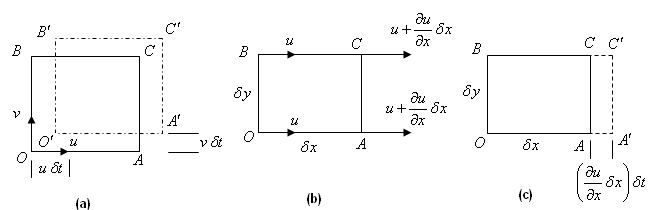
Fig. 3.2.3: Linear deformation of a fluid element.

Rate at which the volume changes per unit volume due to the velocity gradient is

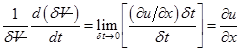(3.2.1)

In the presence of other velocity gradients , Eq. (3.2.1) becomes,

(3.2.2)

If we look closely to the unit of velocity gradients , then they resemble to unit of strain rate and the deformation is associated in the respective directions of orthogonal coordinates in which the components of the velocity lie. Thus, the linear strain (Fig. 3.2.2-a) is defined as the rate of increase in length to original length and the linear strain rates are expressed as,

(3.2.3)

The volumetric strain rate/volumetric dilatation rate is defined as the rate of increase of volume of a fluid element per unit volume.

(3.2.3)

In an incompressible fluid, the volumetric dilatation rate is zero because the fluid element volume cannot change without change in fluid density.