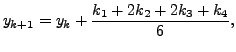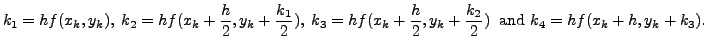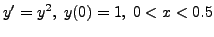We are now ready to state the algorithm for using the Runge-Kutta method of order 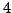 .
This is a generalization of the R-K method of order
.
This is a generalization of the R-K method of order 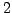 to higher order methods. Without
getting into analytical details, we state the R-K method of order
to higher order methods. Without
getting into analytical details, we state the R-K method of order 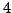 . It is widely used
algorithm. For the IVPs (
. It is widely used
algorithm. For the IVPs (![[*]](crossref.png) ), set
), set
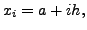 for
for
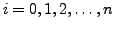 where
where
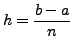 . Also, we set
. Also, we set
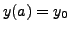 . The for
. The for
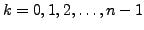 , we define
, we define
where
Remark 14.3.2
The local error in the R-K method of order 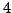 is
is 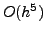 . To achieve this error, we are forced to do
more computation or in other words, spend more time to compute
. To achieve this error, we are forced to do
more computation or in other words, spend more time to compute
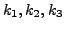 and
and 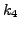 . It all depends
on the nature of the function to estimate the time consumed for the computation. The cost we pay for higher
accuracy is more computation. Also, to reduce the local error, we need smaller values of the step size
. It all depends
on the nature of the function to estimate the time consumed for the computation. The cost we pay for higher
accuracy is more computation. Also, to reduce the local error, we need smaller values of the step size
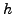 , which again results in large number of computation. Each computation leads to more of rounding errors.
In other words, reduction in discretisation error may lead to increase in rounding off error. THE MORAL IS THAT THE INDISCRIMINATE REDUCTION OF STEP-SIZE NEED NOT MEAN MORE ACCURACY.
, which again results in large number of computation. Each computation leads to more of rounding errors.
In other words, reduction in discretisation error may lead to increase in rounding off error. THE MORAL IS THAT THE INDISCRIMINATE REDUCTION OF STEP-SIZE NEED NOT MEAN MORE ACCURACY.
Figure:
Flow-Chart of Runge-Kutta method of order 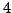
![\includegraphics[scale=.7]{flowchart_4.eps}](img5646.png) |
EXERCISE 14.3.3
Use the Runge-Kutta method of order 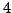 to find an approximate solution of the IVP
to find an approximate solution of the IVP
with step size 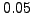 . Also, calculate
the error and tabulate the results.
. Also, calculate
the error and tabulate the results.
A K Lal
2007-09-12
![[*]](crossref.png) ), set
), set
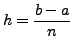 . Also, we set
. Also, we set