For the IVP (![[*]](crossref.png) ) or (
) or (![[*]](crossref.png) ), let
), let
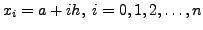 where
where 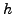 is a given prescribed step size. For
is a given prescribed step size. For
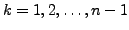 , define
, define 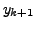 by
by
Then the flow chart associated with the R-K method of order 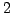 is
is
Figure:
Flow-Chart of Runge-Kutta method of order 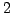
![\includegraphics[scale=.7]{flowchart_3.eps}](img5629.png) |
Solution: Comparing the given IVP with (![[*]](crossref.png) ), we note that
), we note that
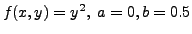 and
and 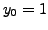 . We now calculate the values of
. We now calculate the values of 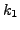 and
and 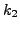 from the R-K method of order
from the R-K method of order 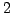 and use
the formula
and use
the formula
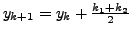 to calculate the approximate values. The results are
shown in Tables
to calculate the approximate values. The results are
shown in Tables ![[*]](crossref.png) and
and ![[*]](crossref.png) .
.
|
|
|
Table 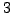
|
|
|
|
|
Initial 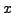
|
Initial 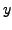
|
Step size 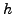
|
Approx 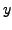
|
Exact 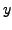
|
Error |
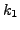
|
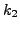
|
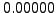
|
1.00000 |
0.10000 |
1.00000 |
1.00000 |
0.00000 |
0.1 |
0.121 |
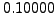
|
1.00000 |
0.10000 |
1.11050 |
1.11111 |
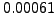
|
0.1 |
0.146531 |
| 0.20000 |
1.11050 |
0.10000 |
1.23377 |
1.25000 |
0.01623 |
0.12332 |
0.18417 |
| 0.30000 |
1.23377 |
0.10000 |
1.338751 |
1.42857 |
0.04106 |
0.15222 |
0.23708 |
| 0.40000 |
1.38751 |
0.10000 |
1.58216 |
1.66667 |
0.08451 |
0.19252 |
0.31495 |
| 0.50000 |
1.58216 |
0.10000 |
1.83589 |
2.00000 |
0.16411 |
0.25032 |
0.00627 |
|
|
|
Table 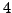
|
|
|
|
|
Initial 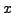
|
Initial 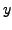
|
Step size 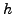
|
Approx 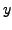
|
Exact 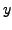
|
Error |
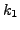
|
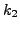
|
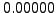
|
1.00000 |
0.05000 |
1.00000 |
1.00000 |
0.00000 |
0.05000 |
0.05513 |
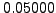
|
1.00000 |
0.05000 |
1.05256 |
1.05263 |
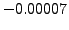
|
0.05539 |
0.06138 |
| 0.10000 |
1.05256 |
0.05000 |
1.11095 |
1.11111 |
 0.00016
0.00016 |
0.06171 |
0.06876 |
| 0.15000 |
1.11095 |
0.05000 |
1.17618 |
1.17647 |
0.00029 |
0.06917 |
0.07755 |
| 0.20000 |
1.17618 |
0.05000 |
1.24954 |
1.25000 |
0.00046 |
0.0781 |
0.08813 |
| 0.25000 |
1.24954 |
0.05000 |
1.33264 |
1.33333 |
0.00070 |
0.08880 |
0.10102 |
| 0.30000 |
1.33264 |
0.05000 |
1.42755 |
1.42857 |
 0.00102
0.00102 |
0.10190 |
0.11696 |
| 0.35000 |
1.42755 |
0.05000 |
1.53697 |
1.53846 |
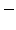 0.00149
0.00149 |
0.11812 |
0.13697 |
| 0.40000 |
1.53697 |
0.05000 |
1.66451 |
1.66667 |
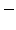 0.00215
0.00215 |
0.13853 |
0.16255 |
| 0.45000 |
1.66451 |
0.05000 |
1.81505 |
1.81818 |
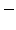 0.00313
0.00313 |
0.16472 |
0.19598 |
| 0.50000 |
1.81505 |
0.05000 |
1.99540 |
2.00000 |
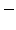 0.00460
0.00460 |
0.199082 |
0.24079 |
A K Lal
2007-09-12
![[*]](crossref.png) ) or (
) or (![[*]](crossref.png) ), let
), let
![]() where
where ![]() is a given prescribed step size. For
is a given prescribed step size. For
![]() , define
, define ![]() by
by
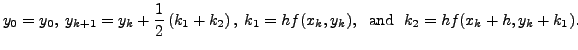
![[*]](crossref.png) ), we note that
), we note that
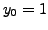 . We now calculate the values of
. We now calculate the values of 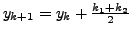 to calculate the approximate values. The results are
shown in Tables
to calculate the approximate values. The results are
shown in Tables ![[*]](crossref.png) and
and ![[*]](crossref.png) .
.