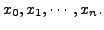Next: A General Quadrature Formula Up: Numerical Differentiation and Integration Previous: Numerical Differentiation Contents
Numerical
Integration is the process of computing the value of a definite
integral,
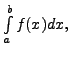 when the values of the
integrand function,
when the values of the
integrand function, ![]() are given at some tabular points.
As in the case of Numerical differentiation, here also the
integrand is first replaced with an interpolating polynomial, and
then the integrating polynomial is integrated to compute the value
of the definite integral. This gives us 'quadrature formula' for
numerical integration. In the case of equidistant tabular points,
either the Newton's formulae or Stirling's formula are used.
Otherwise, one uses Lagrange's formula for the interpolating
polynomial. We shall consider below the case of equidistant
points:
are given at some tabular points.
As in the case of Numerical differentiation, here also the
integrand is first replaced with an interpolating polynomial, and
then the integrating polynomial is integrated to compute the value
of the definite integral. This gives us 'quadrature formula' for
numerical integration. In the case of equidistant tabular points,
either the Newton's formulae or Stirling's formula are used.
Otherwise, one uses Lagrange's formula for the interpolating
polynomial. We shall consider below the case of equidistant
points: