next up previous contents
Next: Numerical Integration Up: Numerical Differentiation and Integration Previous: Introduction   Contents

Numerical Differentiation

In the case of differentiation, we first write the interpolating formula on the interval $ (x_0,x_n).$ and the differentiate the polynomial term by term to get an approximated polynomial to the derivative of the function. When the tabular points are equidistant, one uses either the Newton's Forward/ Backward Formula or Sterling's Formula; otherwise Lagrange's formula is used. Newton's Forward/ Backward formula is used depending upon the location of the point at which the derivative is to be computed. In case the given point is near the mid point of the interval, Sterling's formula can be used. We illustrate the process by taking (i) Newton's Forward formula, and (ii) Sterling's formula.

Recall, that the Newton's forward interpolating polynomial is given by


$\displaystyle f(x)=f(x_{0}+hu)$ $\displaystyle \approx$ $\displaystyle y_0+ {\Delta y_0}u+\frac{\Delta ^2 y_0}{2!}(u(u-1)) + \cdots + \frac{\Delta ^k y_0}{k! } \{u(u-1)\cdots(u-k+1)\}$  
    $\displaystyle + \cdots +\frac{\Delta^n y_0}{n! }\{u(u-1)...(u-n+1)\}.$ (13.2.1)

Differentiating (13.2.1), we get the approximate value of the first derivative at $ x$ as

$\displaystyle \frac{df}{dx} = \frac{1}{h} \frac{df}{du}$ $\displaystyle \approx$ $\displaystyle \frac{1}{h} \left[{\Delta y_0}+\frac{\Delta ^2 y_0}{2!}(2u-1) + \frac{\Delta ^3 y_0}{3!}(3u^{2}-6u+2)+ \cdots \right.$  
    $\displaystyle + \left. \frac{\Delta^n y_{0}}{n! } \left( n u^{n-1} - \frac{n(n-1)^{2}}{2} u^{n-2} + \cdots +(-1)^{(n-1)}(n-1)! \right)\right].$ (13.2.2)

where, $ u=\displaystyle\frac{x-x_0}{h}.$

Thus, an approximation to the value of first derivative at $ x = x_0$ i.e. $ u = 0$ is obtained as :

$\displaystyle \left. \frac{df}{dx}\right\vert _{x=x_0}= \frac{1}{h} \left[{\De... ...ac{\Delta ^3 y_0}{3}- \cdots + (-1)^{(n-1)} \frac{\Delta ^n y_{0}}{n }\right].$ (13.2.3)

Similarly, using Stirling's formula:
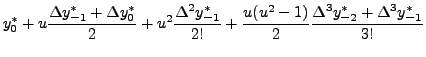$\displaystyle f(x_0^*+hu)$ $\displaystyle \approx$ $\displaystyle y_{0}^*+u\frac{\Delta y_{-1}^*+\Delta y_0^*}{2}+u^2\frac{\Delta^2y_{-1}^* }{2!}+\frac { u(u^2-1)}{2}\frac{\Delta^3 y_{-2}^*+\Delta^3 y_{-1}^* }{3!}$  
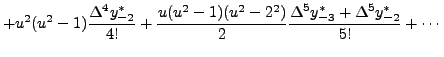    $\displaystyle + u^2(u^2-1)\frac{\Delta^4 y_{-2}^* }{4!}+ \frac{u(u^2-1)(u^2-2^2)}{2} \frac{\Delta^5 y_{-3}^* +\Delta^5 y_{-2}^*}{5!}+ \cdots$ (13.2.4)

Therefore,
$\displaystyle \frac{df}{dx}$ $\displaystyle =$ $\displaystyle \frac{1}{h}\frac{df}{du} \approx \frac{1}{h}\left[\frac{\Delta y_... ...\frac{(3u^2-1)}{2}\times\frac{(\Delta^3 y_{-2}^*+\Delta^3 y_{-1}^*)}{3!}\right.$  
    $\displaystyle + 2u(2u^2-1)\frac{\Delta^4 y_{-2}^*}{4!}\left.+\frac{(5u^4-15u^2+4)(\Delta^5y_{-3}^* +\Delta^5 y_{-2}^*)}{2\times 5!}+\cdots\right]$ (13.2.5)

Thus, the derivative at $ x=x_0^*$ is obtained as:

$\displaystyle \left. \frac{df}{dx}\right\vert _{x=x_{0}^*}= \frac{1}{h} \left[... ...\frac{4\times(\Delta^5y_{-3}^* +\Delta^5 y_{-2}^*)}{2\times 5!}+\cdots\right].$ (13.2.6)

Remark 13.2.1   Numerical differentiation using Stirling's formula is found to be more accurate than that with the Newton's difference formulae. Also it is more convenient to use.

Now higher derivatives can be found by successively differentiating the interpolating polynomials. Thus e.g. using (13.2.2), we get the second derivative at $ x = x_0$ as

$\displaystyle \left. \frac{d^2f}{dx^2}\right\vert _{x=x_0}= \frac{1}{h^2} \le... ..._0}-{\Delta ^3 y_0} + \frac{2\times11\times\Delta ^4 y_0}{4!}- \cdots\right]. $

EXAMPLE 13.2.2   Compute from following table the value of the derivative of $ y=f(x)$ at $ x=1.7489$ :
$ x$ 1.73 1.74 1.75 1.76 1.77
$ y$ 1.772844100 1.155204006 1.737739435 1.720448638 1.703329888
Solution: We note here that $ x_0 = 1.75, h= 0.01,$ so $ u = (1.7489-1.75)/0.01 = -0.11$ , and $ \Delta y_0 = -.0017290797, \Delta^2 y_{0}= .0000172047,\Delta^3 y_{0} = -.0000001712,$
$ \Delta y_{-1} = -.0017464571, \Delta^2 y_{-1}= .0000173774,\Delta^3 y_{-1} = -.0000001727,$
$ \Delta^3 y_{-2} = -.0000001749, \Delta^4 y_{-2} = -.0000000022$
Thus, $ f'(1.7489)$ is obtained as:
(i) Using Newton's Forward difference formula,
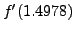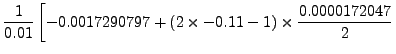$\displaystyle f'(1.4978)$ $\displaystyle \approx$ $\displaystyle \frac{1}{0.01}\left[ -0.0017290797 + (2\times-0.11 - 1)\times\frac{0.0000172047}{2}\right.$  
    $\displaystyle + \left.(3\times(-0.11)^2 - 6\times-0.11+2)\times\frac{ -0.0000001712}{3!}\right]= -0.173965150143.$  

(ii) Using Stirling's formula, we get:
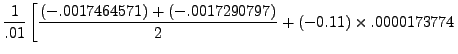$\displaystyle f'(1.4978)$ $\displaystyle \approx$ $\displaystyle \frac{1}{.01} \left[\frac{(-.0017464571)+(-.0017290797)}{2}+(-0.11)\times .0000173774 \right.$  
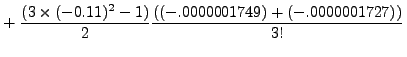    $\displaystyle + \left. \frac{(3\times(-0.11)^2 -1)}{2}\frac{((-.0000001749 )+ (-.0000001727))}{3!}\right.$  
    $\displaystyle +\left. 2\times(-0.11)\times(2(-0.11)^2-1)\times \frac{(-.0000000022)}{4!} \right]$  
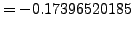    $\displaystyle = -0.17396520185$  

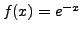It may be pointed out here that the above table is for $ f(x) = e^{-x}$ , whose derivative has the value -0.1739652000 at $ x = 1.7489. $

EXAMPLE 13.2.3   Using only the first term in the formula (13.2.6) show that

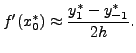
$\displaystyle f'(x_{0}^*) \approx \frac{y_{1}^* - y_{-1}^*}{2h}.$

Hence compute from following table the value of the derivative of $ y = e^x$ at $ x=1.15$ :
$ x$ 1.05 1.15 1.25
$ e^x$ 2.8577 3.1582 3.4903
Solution: Truncating the formula (13.2.6)after the first term, we get:
$\displaystyle f'(x_{0}^*)$ $\displaystyle \approx$ $\displaystyle \frac{1}{h}\left[\frac{\Delta y_{-1}^*+ \Delta y_0^*}{2}\right]$  
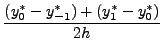  $\displaystyle =$ $\displaystyle \frac{(y_0^*-y_{-1}^*)+(y_1^*-y_{0}^*)}{2h}$  
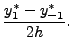  $\displaystyle =$ $\displaystyle \frac{y_{1}^* - y_{-1}^*}{2h}.$  

Now from the given table, taking $ x_0^*= 1.15$ , we have

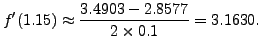
$\displaystyle f'(1.15) \approx \frac{3.4903 - 2.8577}{2\times0.1}=3.1630.$

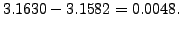
Note the error between the computed value and the true value is $ 3.1630 - 3.1582 = 0.0048.$

EXERCISE 13.2.4   Retaining only the first two terms in the formula (13.2.3), show that

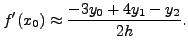
$\displaystyle f'(x_{0})\approx \frac{ -3 y_{0} + 4 y_{1}- y_{2}}{2h}.$

Hence compute the derivative of $ y = e^x$ at $ x=1.15$ from the following table:
$ x$ 1.15 1.20 1.25
$ e^x$ 3.1582 3.3201 3.4903
Also compare your result with the computed value in the example (13.2.3).

EXERCISE 13.2.5   Retaining only the first two terms in the formula (13.2.6), show that

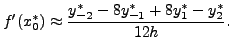
$\displaystyle f'(x_{0}^*) \approx \frac{y_{-2}^* -8 y_{-1}^*+8 y_{1}^*- y_{2}^*}{12h}.$

Hence compute from following table the value of the derivative of $ y = e^x$ at $ x=1.15$ :
$ x$ 1.05 1.10 1.15 1.20 1.25
$ e^x$ 2.8577 3.0042 3.1582 3.3201 3.4903

EXERCISE 13.2.6   Following table gives the values of $ y=f(x)$ at the tabular points $ x = 0 + 0.05 \times k$ , $ k = 0,1,2,3,4,5.$
$ x$ 0.00 0.05 0.10 0.15 0.20 0.25
$ y$ 0.00000 0.10017 0.20134 0.30452 0.41075 0.52110
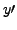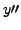Compute (i)the derivatives $ y\prime$ and $ y\prime\prime$ at $ x=0.0$ by using the formula (13.2.2). (ii)the second derivative $ y\prime\prime$ at $ x=0.1$ by using the formula (13.2.6).

 Similarly, if we have tabular points which are not equidistant, one can use Lagrange's interpolating polynomial, which is differentiated to get an estimate of first derivative. We shall see the result for four tabular points and then give the general formula. Let $ x_0, x_1, x_2, x_3$ be the tabular points, then the corresponding Lagrange's formula gives us:
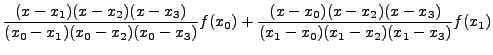$\displaystyle f(x)$ $\displaystyle \approx$ $\displaystyle \frac{(x-x_1)(x-x_2)(x -x_{3})}{(x_0-x_1)(x_0-x_2)(x_0 - x_{3})}f(x_0) + \frac{(x-x_0)(x-x_2)(x - x_{3})}{(x_1-x_0)(x_1-x_2)(x_1 - x_{3})}f(x_1)$  
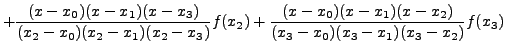    $\displaystyle + \frac{(x-x_0)(x-x_1)(x- x_{3})}{(x_{2}-x_0)(x_{2}-x_1)(x_{2} - ... ...+\frac{(x-x_0)(x-x_1)(x- x_{2})}{(x_{3}-x_0)(x_{3}-x_1)(x_{3} - x_{2})}f(x_{3})$  

Differentiation of the above interpolating polynomial gives:
$\displaystyle \frac{df(x)}{dx}$ $\displaystyle \approx$ $\displaystyle \frac{(x-x_2)(x-x_3)+(x-x_1)(x -x_{2})+(x-x_1)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0 - x_{3})}f(x_0)$  
    $\displaystyle + \frac{(x-x_2)(x-x_3)+(x-x_0)(x -x_2)+(x-x_0)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1 - x_{3})}f(x_1)$  
    $\displaystyle + \frac{(x-x_1)(x-x_2)+(x-x_0)(x -x_{1})+(x-x_0)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2 - x_{3})}f(x_2)$  
    $\displaystyle + \frac{(x-x_1)(x-x_2)+(x-x_0)(x -x_{2})+(x-x_0)(x-x_1)}{(x_3-x_0)(x_3-x_1)(x_3 - x_{2})}f(x_3)$  
  $\displaystyle =$ $\displaystyle \Bigl( \prod\limits_{r=0}^{3} (x - x_r)\Bigr) \left[\sum_{i=0}^{3... ...^{3} (x_i - x_j)}\left(\sum_{k=0,\;k\neq i}^{3}\frac{1}{(x-x_k)}\right)\right].$ (13.2.7)

In particular, the value of the derivative at $ x = x_0$ is given by


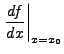$\displaystyle \left. \frac{df}{dx}\right\vert _{x=x_0}$ $\displaystyle \approx$ $\displaystyle \left[ \frac{1}{(x_0-x_1)}+\frac{1}{(x_0-x_2)}+ \frac{1}{(x_0 - x... ...ight] f(x_0)+ \frac{(x_0-x_2)(x_0-x_3)}{(x_1-x_0)(x_1-x_2)(x_1 - x_{3})} f(x_1)$  
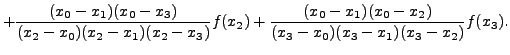    $\displaystyle + \frac{(x_0-x_1)(x_0-x_3)}{(x_2-x_0)(x_2-x_1)(x_2 - x_{3})} f(x_2)+ \frac{(x_0-x_1)(x_0-x_2)}{(x_3-x_0)(x_3-x_1)(x_3 - x_{2})} f(x_3).$  

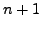Now, generalizing Equation (13.2.7) for $ n+1$ tabular points 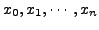$ x_0, x_1,\cdots, x_n$ we get:
$\displaystyle \frac{df}{dx}$ $\displaystyle =$ $\displaystyle \prod\limits_{r=0}^{n} (x - x_r) \left[\sum_{i=0}^{n} \frac{ f(x_... ...^{n} (x_i - x_j)}\left(\sum_{k=0,\;k\neq i}^{n}\frac{1}{(x-x_k)}\right)\right].$  

EXAMPLE 13.2.7   Compute from following table the value of the derivative of $ y=f(x)$ at $ x=0.6$ :
$ x$ 0.4 0.6 0.7
$ y$ 3.3836494 4.2442376 4.7275054
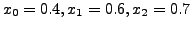Solution: The given tabular points are not equidistant, so we use Lagrange's interpolating polynomial with three points: $ x_0 =0.4, x_1= 0.6, x_2= 0.7$ . Now differentiating this polynomial the derivative of the function at $ x = x_1$ is obtained in the following form:

$\displaystyle \left. \frac{df}{dx}\right\vert _{x=x_1}\approx \frac{(x_1-x_2)... ...+\frac{1}{(x_1-x_0)}\right]f(x_1)+ \frac{(x_1-x_0)}{(x_2-x_0)(x_2-x_1)}f(x_2).$

Note: The reader is advised to derive the above expression.
Now, using the values from the table, we get:
$\displaystyle \left. \frac{df}{dx}\right\vert _{x=0.6}$ $\displaystyle \approx$ $\displaystyle \frac{(0.6-0.7)}{(0.4-0.6)(0.4-0.7)}\times 3.3836494 +\left[\frac{1}{(0.6 - 0.7)}+\frac{1}{(0.6 - 0.4)}\right]\times 4.2442376$  
    $\displaystyle + \frac{(0.6-0.4)}{(0.7 -0.4)(0.7- 0.6 )}\times 4.7225054$  
  $\displaystyle =$ $\displaystyle -5.63941567- 21.221188 + 31.48336933 = 4.6227656 .$  

For the sake of comparison, it may be pointed out here that the above table is for the function $ f(x)=2e^x+ x$ , and the value of its derivative at $ x=0.6$ is $ 4.6442376.$

EXERCISE 13.2.8   For the function, whose tabular values are given in the above example(13.2.8), compute the value of its derivative at $ x=0.5.$

Remark 13.2.9   It may be remarked here that the numerical differentiation for higher derivatives does not give very accurate results and so is not much preferred.

next up previous contents
Next: Numerical Integration Up: Numerical Differentiation and Integration Previous: Introduction   Contents
A K Lal 2007-09-12