Next: Numerical Methods Up: Numerical Integration Previous: Trapezoidal Rule Contents
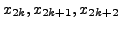 and so the integrand is replaced with
a quadratic interpolating polynomial. Thus using the formula
(13.3.3), we get,
and so the integrand is replaced with
a quadratic interpolating polynomial. Thus using the formula
(13.3.3), we get,
![$\displaystyle \int\limits^{x_{2k+2}}_{x_{2k}}f(x)dx = \frac{h}{3}\left[y_{2k}
+ 4 y_{2k+1} + y_{2k+2} \right].$](img5485.png)
In view of this, we have
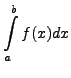 |
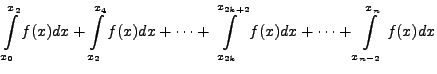 |
||
![$\displaystyle \frac{h}{3}\left[(y_{0} +
4 y_{1} + y_{2})+(y_{2} + 4 y_{3} + y_{4})+ \cdots+ (y_{n-2} + 4
y_{n-1} + y_{n}) \right]$](img5487.png) |
|||
![$\displaystyle \frac{h}{3}\left[y_{0} + 4 y_{1} + 2
y_{2}+ 4 y_{3} + 2 y_{4}+ \cdots+ 2 y_{n-2} + 4 y_{n-1} + y_{n}
\right],$](img5488.png) |
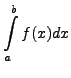 |
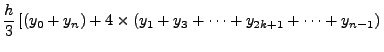 |
||
![$\displaystyle \frac{h}{3}\left[(y_{0} +y_{n})+ 4\times\left(\sum_{i=1,\; i - od...
...1}y_{i}\right) + 2\times\left(\sum_{i=2,\; i - even
}^{n-2}y_{i}\right)\right].$](img5491.png) |
(13.3.5) |
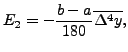 |
(13.3.6) |
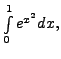 by Simpson's rule. Also estimate
the error in its calculation and compare it with the error using
Trapezoidal rule.
by Simpson's rule. Also estimate
the error in its calculation and compare it with the error using
Trapezoidal rule.
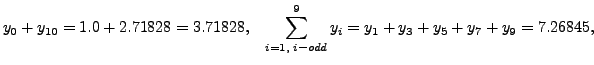
and
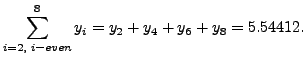
Thus,
![$\displaystyle \int\limits^{1}_{0}e^{x^2}dx= \frac{0.1}{3}\times[3.71828 +
4\times7.268361+ 2\times5.54412 ]=1.46267733$](img5497.png)
To find the error estimates, we consider the forward difference table, which is given below:
|
|
|
|
|
|
|
||
| 0.0 | 1.00000 | 0.01005 | 0.02071 | 0.00189 | 0.00149 | ||
| 0.1 | 1.01005 | 0.03076 | 0.02260 | 0.00338 | 0.00171 | ||
| 0.2 | 1.04081 | 0.05336 | 0.02598 | 0.00519 | 0.00243 | ||
| 0.3 | 1.09417 | 0.07934 | 0.03117 | 0.00762 | 0.00320 | ||
| 0.4 | 1.17351 | 0.11051 | 0.3879 | 0.01090 | 0.00459 | ||
| 0.5 | 1.28402 | 0.14930 | 0.04969 | 0.01549 | 0.00658 | ||
| 0.6 | 1.43332 | 0.19899 | 0.06518 | 0.02207 | 0.00964 | ||
| 0.7 | 1.63231 | 0.26417 | 0.08725 | 0.03171 | |||
| 0.8 | 1.89648 | 0.35142 | 0.11896 | ||||
| 0.9 | 2.24790 | 0.47038 | |||||
| 1.0 | 2.71828 |
Thus, error due to Trapezoidal rule is,
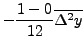 |
|||
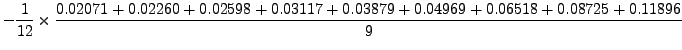 |
|||
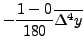 |
|||
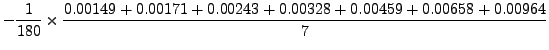 |
|||
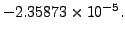 |
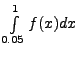 , where the
table for the values of
, where the
table for the values of |
|
0.05 | 0.1 | 0.15 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
|
|
0.0785 | 0.1564 | 0.2334 | 0.3090 | 0.4540 | 0.5878 | 0.7071 | 0.8090 | 0.8910 | 0.9511 | 0.9877 | 1.0000 |
Solution: Note that here the points are not given to be
equidistant, so as such we can not use any of the above two
formulae. However, we notice that the tabular points
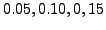 and
and ![]() are equidistant and so are the tabular points
are equidistant and so are the tabular points
![]() and
and ![]() . Now we can
divide the interval in two subinterval:
. Now we can
divide the interval in two subinterval:
![]() and
and
![]() ; thus,
; thus,
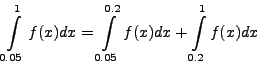
. The integrals then can be evaluated in each interval. We observe that the second set has odd number of points. Thus, the first integral is evaluated by using Trapezoidal rule and the second one by Simpson's rule (of course, one could have used Trapezoidal rule in both the subintervals).
![$\displaystyle \int\limits^{0.2}_{0.05}f(x)dx =
0.05\times\left[\frac{0.0785+0.3090}{2}+0.1564+0.2334\right]=
0.0291775,$](img5516.png)
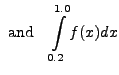 |
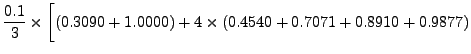 |
||
![$\displaystyle \hspace{1in} \biggl. +2\times( 0.5878+0.8090+
0.9511)\biggr]$](img5519.png) |
|||
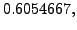 |
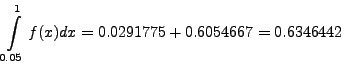
It may be mentioned here that in the above integral,
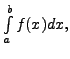 where the table for the values of
where the table for the values of 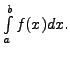 Also get an error estimate of the computed integral.
Also get an error estimate of the computed integral.
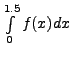 , where the
table for the values of
, where the
table for the values of | 0.0 | 0.5 | 0.7 | 0.9 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | ||
| 0.00 | 0.39 | 0.77 | 1.27 | 1.90 | 2.26 | 2.65 | 3.07 | 3.53 |