Let
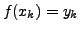 be the nodal value at the tabular point
be the nodal value at the tabular point 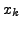 for
for
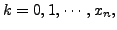 where
where 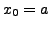 and
and
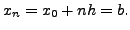 Now, a general quadrature formula is obtained by replacing the
integrand by Newton's forward difference interpolating polynomial.
Thus, we get,
Now, a general quadrature formula is obtained by replacing the
integrand by Newton's forward difference interpolating polynomial.
Thus, we get,
This on using the transformation
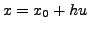 gives:
gives:
which on term by term integration gives,
For 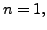 i.e., when linear interpolating polynomial is
used then, we have
i.e., when linear interpolating polynomial is
used then, we have
![$\displaystyle \int\limits^{b}_{a}f(x)dx = h\left[y_0+\frac{\Delta y_0}{2}\right]=\frac{h}{2} \left[y_0 +y_1\right].$](img5460.png) |
(13.3.2) |
Similarly, using interpolating polynomial of degree 2 (i.e. 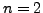 ), we obtain,
), we obtain,
In the above we have replaced the integrand by an interpolating
polynomial over the whole interval ![$ [a, b]$](img5463.png) and then integrated it
term by term. However, this process is not very useful. More
useful Numerical integral formulae are obtained by dividing the
interval
and then integrated it
term by term. However, this process is not very useful. More
useful Numerical integral formulae are obtained by dividing the
interval ![$ [a, b]$](img5463.png) in
in 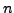 sub-intervals
sub-intervals
![$ [x_k, x_{k+1}],$](img5464.png) where,
where,
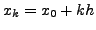 for
for
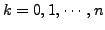 with
with
A K Lal
2007-09-12
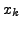 for
for
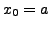 and
and
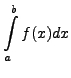
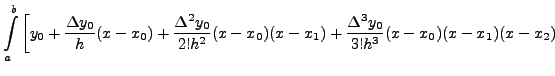
![$\displaystyle + \left.\frac{\Delta^4
y_0}{4!h^4}(x-x_0)(x-x_1)(x-x_2)(x-x_3)+ \cdots \right]dx$](img5454.png)
![]() gives:
gives:
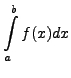
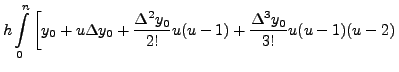
![$\displaystyle + \left.\frac{\Delta^4
y_0}{4!}u(u-1)(u-2)(u-3)+ \cdots \right]du$](img5457.png)