| 19.1.2 |
Theorem: |
| |
Proof: |
| |
To prove (iv), we first note that for 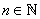 , by (iii), we have , by (iii), we have
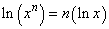 . .
Hence,
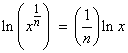 . .
Also,
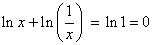 . .
Thus
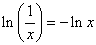 . .
Hence, for every 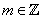 , ,
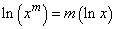 . .
Finally, if 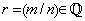 , then , then
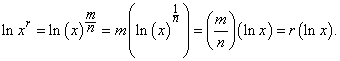
To prove (v). Note that
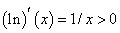
Thus, 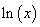 is strictly increasing. Further, is strictly increasing. Further,
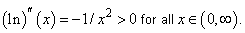
Hence, 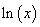 is a concave function. is a concave function. |
| |
Proof continued.. |
| |
 
|
|