To prove (vi), we first note that
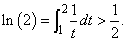
Thus, using(iv), we get
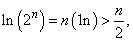
and hence,
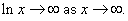
Further, this together with the fact that 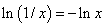 , implies that , implies that
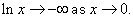
In particular, given any 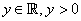 we can find we can find 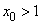 such that such that
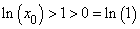
Thus, by the intermediate property for continuous functions,
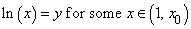
Hence, 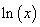 is an onto function is an onto function  Back Back
|