Recall, that in elementary calculus, one uses the formula
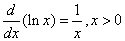 , ,
without really knowing the function 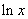 . We can use this formula, and the fundamental theorem of calculus, to define the . We can use this formula, and the fundamental theorem of calculus, to define the 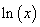 . Since the function . Since the function 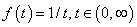 is continuous on is continuous on 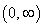 , it is integrable, i.e., , it is integrable, i.e., 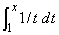 exists for every exists for every 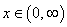 . This motivate our definition: . This motivate our definition:
|