The exponential function, denoted by exp is the one-one, onto function 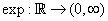 such that such that
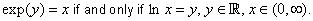
The exponential function, as defined above is also called the exponential function to the natural base. The properties of the exponential function are given in the next theorem. |