Let 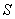 be an oriented surface with the continuous unit normal be an oriented surface with the continuous unit normal 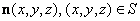 . Let . Let 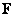 be a continuous vector field on be a continuous vector field on 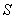 . Then the integral . Then the integral
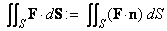
is called the flux-integral of 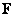 over the surface over the surface 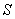 . .
Physically, 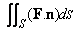 represents the flux of the fluid with flux density represents the flux of the fluid with flux density 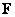 across the surface across the surface 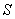 in the direction of the chosen normal. in the direction of the chosen normal. |