In order to be able to do so, it becomes necessary to ensure that the function
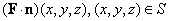
is integrable over 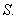 For example, this will be so if For example, this will be so if 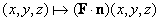 is continuous. For this, we can assume that is continuous. For this, we can assume that 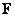 is continuous. Thus, to be able to define is continuous. Thus, to be able to define 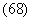 , we should be able to say that our surface , we should be able to say that our surface 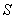 is such that at every point is such that at every point 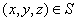 , three exist unit normal , three exist unit normal 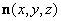 which varies continuously as which varies continuously as 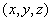 very over very over 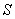 . This motivates our next definition: . This motivates our next definition:
|