Similar to the integral of a scalar field over a curve, which we called the line integral, we can define the integral of a vector-field over a surface.
Let 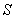 be a surface in space with finite surface area. Let be a surface in space with finite surface area. Let 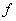 be a continuous scalar-field defined on the surface be a continuous scalar-field defined on the surface 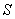 .We can subdivide .We can subdivide 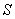 into smaller portions, say into smaller portions, say 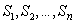 having areas having areas 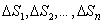 , and form the sum , and form the sum
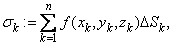
|