| |
Consider the sequence 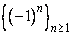 . We showed in example 2.2.2(iii) that this sequence in not convergent. Clearly, it is a bounded sequence as . We showed in example 2.2.2(iii) that this sequence in not convergent. Clearly, it is a bounded sequence as 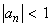 for every n . for every n .
However, it not always easy to guess whether a sequence is convergent or not and even if it is convergent, what is its limit. We describe in next section in next section some theorems which helps us to compute limits of sequences. |