| |
then  , ,
 . .
Hence,  . .
Click here to View the Interactive animation : Applet 1.6 |
(ii)
|
The sequence  is not convergent. is not convergent.
Suppose,  . Then given . Then given , there exists , there exists  such that such that
 , ,
i.e.,
 , ,
which is not true (Archimedian property). In some sense  is not convergent as it outgrows every real number. is not convergent as it outgrows every real number.
In fact, if a sequence is convergent, it can not grow arbitrarily, as we shall see in the next section. |
(iii)
|
Consider the sequence 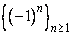 . Every odd term of the sequence is . Every odd term of the sequence is  and every even term of the sequence is and every even term of the sequence is  . Intuitively, the elements . Intuitively, the elements 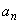 do not come closer to a single value do not come closer to a single value  . We expect . We expect 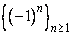 to be divergent. We can write it as follows. First suppose to be divergent. We can write it as follows. First suppose  . If . If 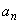   then given then given  , there should exist some , there should exist some  such that such that |