| |
The aim of this lecture is to analyze various concepts about sequences: a sequence being bounded, monotone, and convergent. |
| |
Given a sequence  , one is interested to know: what happens to , one is interested to know: what happens to 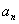 as as 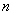 becomes large. In the example of the area of the unit circle, we expect that for n sufficiently large, becomes large. In the example of the area of the unit circle, we expect that for n sufficiently large,  will be a 'good enough' representation of will be a 'good enough' representation of
 , the area of the unit circle, that is, will , the area of the unit circle, that is, will  come close to the value come close to the value  , the area of the unit circle when n becomes large? How close? Will it come as close as we want? Using the concept of absolute value (which gives the notion of distance on , the area of the unit circle when n becomes large? How close? Will it come as close as we want? Using the concept of absolute value (which gives the notion of distance on  ) we can express it mathematically as follows: ) we can express it mathematically as follows: |
| |
If we consider the geometric visualization of the sequence  as a function, as a function,  then saying that the number then saying that the number  will be the limit of the sequence means that given any horizontal strip, of width will be the limit of the sequence means that given any horizontal strip, of width 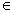 centered at centered at  , all but finitely many of , all but finitely many of  lie in this strip.
Intuitively, after some stage all the elements of the sequence are close to lie in this strip.
Intuitively, after some stage all the elements of the sequence are close to  . Or a 'tail' of the convergent sequence lies inside any small neighborhood of . Or a 'tail' of the convergent sequence lies inside any small neighborhood of  . A sequence which is not convergent is called a divergent sequence. . A sequence which is not convergent is called a divergent sequence. |