 |
Thus the force on the conductor in this section is 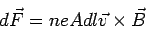
If 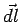 represents a vector whose magnitude is the length of the segment and whose direction is along the direction of represents a vector whose magnitude is the length of the segment and whose direction is along the direction of 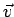 , we may rewrite the above as , we may rewrite the above as
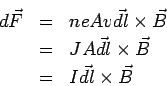
The net force on the conductor is given by summing over all the length elements. If 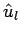 denotes a unit vector in the direction of the current, then denotes a unit vector in the direction of the current, then 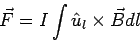
Example 1 Example 2 Example 3 |