| |
The work done is given by
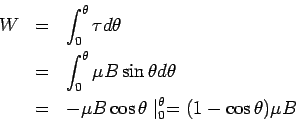
This amount of work is stored as the additional potential energy of the dipole. In analogy with the case of electric dipole in an electric field, the potential energy of the magnetic dipole in a magnetic field is given by
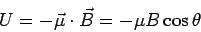
The energy is lowest when 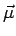 and and 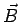 are along the same direction and is maximum when they are anti-parallel. are along the same direction and is maximum when they are anti-parallel. |