Module 3 : MAGNETIC FIELD
Lecture 14 : Force on a Current Carrying Conductor
Example 3 :
  Force on a conductor of arbitrary shape in a uniform field
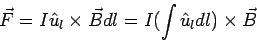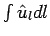  For an wire of arbitrary shape,  \begin{displaymath}\vec F = I\hat u_l\times\vec B dl = I (\int \hat u_l dl)\times\vec B\end{displaymath}
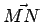  Now, $\int \hat u_l dl$is the sum of vectors along the curve from the initial point M to the final point N. By law of vector addition, the sum is equal to the vector $\vec{MN}$connecting the two end points by a straightline segment. Thus
 
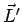\begin{displaymath}\vec F = I (\vec L^\prime\times\vec B)\end{displaymath}
  where $\vec L^\prime$is the vector connecting the two end points. (Using this, the result of the previous example trivially follows).
 
\includegraphics{fig3.10.eps}
  Corollary : The force on a closed current loop in a constant magnetic field is zero.

          Back