| |
A unit vector in any direction has a magnitude (length) 1. The unit vectors parallel to the cartesian 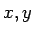 and and 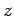 coordinates are usually designated by coordinates are usually designated by 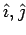 and and 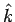 respectively. In terms of these unit vectors, the vector respectively. In terms of these unit vectors, the vector 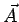 is written is written |
| |
|
| |
Any vector in 3 dimension may be written in this fashion. The vectors 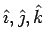 are said to form a basis . In fact, any three non-colinear vectors may be used as a basis. The basis vectors used here are perpendicular to one another. A unit vector along the direction of are said to form a basis . In fact, any three non-colinear vectors may be used as a basis. The basis vectors used here are perpendicular to one another. A unit vector along the direction of 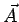 is is |
| |
|
| |
|
|