| |
In the figure P is the foot of the perpendicular drawn from the tip of the position vector on to the x-y plane. Since the axis of rotation coincides with the z-axis, the z coordinate does not change and we have 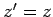 . The figure shows various angles to be equal to the angle of rotation . The figure shows various angles to be equal to the angle of rotation 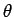 by use of simple geometry. One can easily see by use of simple geometry. One can easily see |
| |
Since any vector can be parallely shifted to the origin, its tranformation properties are identical to the transformation properties of the position vector. Thus under rotation of coordinate system by an angle 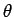 about the z-axis the components of a vector about the z-axis the components of a vector 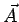 transform as follows : transform as follows : |