| |
SCALAR AND VECTOR FIELDS |
| |
This introductory chapter is a review of mathematical concepts required for the course. It is assumed that the reader is already familiar with elementary vector analysis. |
| |
Physical quantities that we deal with in electromagnetism can be scalars or vectors.
A scalar is an entity which only has a magnitude. Examples of scalars are mass, time, distance, electric charge, electric potential, energy, temperature etc.
A vector is characterized by both magnitude and direction. Examples of vectors in physics are displacement, velocity, acceleration, force, electric field, magnetic field etc. |
| |
A field is a quantity which can be specified everywhere in space as a function of position. The quantity that is specified may be a scalar or a vector. For instance, we can specify the temperature at every point in a room. The room may, therefore, be said to be a region of ``temperature field" which is a scalar field because the temperature 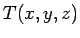 is a scalar function of the position. An example of a scalar field in electromagnetism is the electric potential. is a scalar function of the position. An example of a scalar field in electromagnetism is the electric potential. |
| |
In a similar manner, a vector quantity which can be specified at every point in a region of space is a vector field. For instance, every point on the earth may be considered to be in the gravitational force field of the earth. we may specify the field by the magnitude and the direction of acceleration due to gravity (i.e. force per unit mass ) 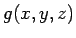 at every point in space. As another example consider flow of water in a pipe. At each point in the pipe, the water molecule has a velocity at every point in space. As another example consider flow of water in a pipe. At each point in the pipe, the water molecule has a velocity 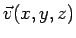 . The water in the pipe may be said to be in a velocity field. There are several examples of vector field in electromagnetism, e.g., the electric field . The water in the pipe may be said to be in a velocity field. There are several examples of vector field in electromagnetism, e.g., the electric field 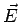 , the magnetic flux density , the magnetic flux density 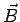 etc. etc. |
| |
|
|