Writing qC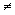 in terms of the vibrational modes (qv) C [ which is approximated as kBT / h in terms of the vibrational modes (qv) C [ which is approximated as kBT / h 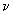 ] and all the other remaining modes [ ] and all the other remaining modes [ 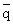 C C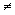 ], we have for qC ], we have for qC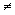 , , |
| qC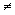 = (kBT / h = (kBT / h 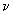 ) ) 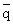 C C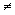
|
(33.26) |
| Combining (33.26), (33.23) and (33.4), we have, |
| |
|
k2 = k 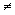 K K 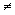 = = 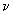 ( RT / p0) K = ( ( RT / p0) K = (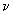 k BT / h k BT / h 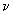 )[ ( NA )[ ( NA 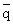 C C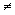 / q A qB) e / q A qB) e 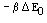 RT / p0 ) RT / p0 ) |
(33.27) |
| |
= kB T / h
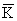 |
(33.28) |
Where 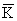 is the second, square bracketed expression in eq (33.27) which is akin to an equilibrium constant. There are often factors not included in (33.27) and they are included through a transmission coefficient is the second, square bracketed expression in eq (33.27) which is akin to an equilibrium constant. There are often factors not included in (33.27) and they are included through a transmission coefficient
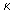 and the rate constant in the transition state theory becomes, and the rate constant in the transition state theory becomes, |
| |
k 2 =
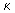 ( kBT / h ) ( kBT / h ) 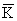 |
(33.29) |
We want to express 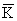 in terms of molecular partition functions. Let us obtain a formula for simple species of A and B where A and B are atoms. The partition function of atoms is simply the translational partition function (as rotations and vibrations are absent). The translational partition function was given earlier in Lecture 29 as in terms of molecular partition functions. Let us obtain a formula for simple species of A and B where A and B are atoms. The partition function of atoms is simply the translational partition function (as rotations and vibrations are absent). The translational partition function was given earlier in Lecture 29 as |
| |
q T = ( 2
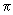 mkBT / h2 ) 3 / 2 V mkBT / h2 ) 3 / 2 V |
(33.30) |
| and using the molar volume, the partition function for A becomes |
q T,A = ( 2 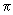 mA kB T / h 2 ) 3 / 2 V 0m mA kB T / h 2 ) 3 / 2 V 0m |
= V 0m /
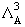 , ,
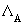 =
h / ( 2 =
h / ( 2 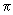 mA kBT)1 / 2 mA kBT)1 / 2 |
(33.31) |
| |
Where V 0m is the standard molar volume, given by RT / p0 and
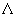 A is called the de Broglie thermal wavelength. For the activated complex, the partition function is the product of translational, vibrational and rotational partition functions, because in our present model, AB is a diatomic. However, we have already considered the vibrational partition function in (33.24) and we need to consider A is called the de Broglie thermal wavelength. For the activated complex, the partition function is the product of translational, vibrational and rotational partition functions, because in our present model, AB is a diatomic. However, we have already considered the vibrational partition function in (33.24) and we need to consider 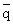 C C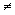 now which includes only translation and rotation . now which includes only translation and rotation . |
| This is given by |
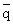 C C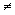 = V 0m / = V 0m /
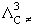 .( 2 I kB T / .( 2 I kB T / 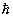 2 ) 2 ) |
(33.32) |
| |