Our next task is the determination of the concentration of C . Let us express the equilibrium constant for the reaction A + B 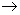 C in terms of the partial pressures of A, B and C (pA , p B and pC ) C in terms of the partial pressures of A, B and C (pA , p B and pC ) |
| |
| K = [ C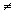 ] / [ A] [ B] = [ p C ] / [ A] [ B] = [ p C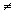 / /
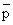 ] / [ ( pA / ] / [ ( pA /
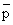 ) ( pB / ) ( pB /
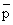 ) ] ) ]
|
(33.6) |
Where 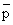 is the standard pressure of 1 bar. These partial pressure can be expressed in terms of molar concentrations of A, B and C as follows. is the standard pressure of 1 bar. These partial pressure can be expressed in terms of molar concentrations of A, B and C as follows. |
| |
| [A] = nA / V ; V = n RT / p; p A = xA p = nA p / n |
| |
| [A] = nA p / nRT = xAp / R T = p A / RT or p A = R T [A] |
(33.7) |
In eq. 33.7, V = total volume, p = total pressure, n = total number of moles, nA = number of moles of A, x A =
nA / n, the mole fraction, RT = gas constant x absolute temperature. |
| Substituting each partial pressure in terms of the mole fractions we have |
| |
K = RT [ C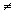 ] / ] /
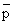 / [(RT [A] / / [(RT [A] /
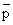 ) (RT [B] / ) (RT [B] /
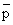 )] )] |
(33.8) |
| |
= [C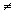 ] ]
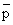 / [A] [B] RT / [A] [B] RT |
(33.9) |
| |
or C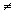 = [A] [B] RT / = [A] [B] RT /
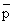 K K |
(33.10) |
| Comparing this equation with eq. (33.3), we have |
| |
or K 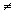 = RT / = RT /
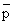 K K |
(33.11) |
In eq (33.3), K 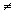 was merely a proportionality constant and now it has been related to the equilibrium constant for the formation of the activated complex. was merely a proportionality constant and now it has been related to the equilibrium constant for the formation of the activated complex. |
| |