| 21.4 |
| Heat Capacities |
The capacity to absorb heat in an infinitesimal increment in temperature,
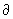 q/ q/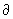 T is referred to as the heat capacity. At constant volume, w = -pdV = 0, U = q and the heat capacity is T is referred to as the heat capacity. At constant volume, w = -pdV = 0, U = q and the heat capacity is |
| |
C V = (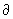 U/ U/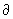 T) V T) V |
(21.6) |
In a constant volume process, 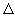 U = q = q V and the change in U for a given change in temperature is given by U = q = q V and the change in U for a given change in temperature is given by |
| 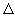 U = U = 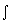 CV dT CV dT
|
(21.7) |
Analogous to the state function U, other useful state functions can be defined. One such function is enthalpy, H and a change in H is 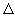 H. Note also that P and V are naturally state functions. H. Note also that P and V are naturally state functions. |
| |
| H =U + PV |
(21.8) |
| |
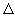 H = H = 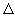 U + U + 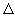 (PV) (PV) |
(21.9) |
| For a constant pressure process, eq (21.9) becomes |
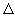 H = q - PdV + d (PV) H = q - PdV + d (PV) |
| = q - PdV + VdP + PdV |
| = q + VdP |
| = q, as dP = 0 |
(21.10) |
i.e., the heat absorbed by the system at constant pressure is equal to the enthalpy change in the process. Similar to CV , we can define a heat capacity at constant pressure Cp by |
| |
Cp = (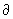 H/ H/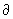 T) p T) p |
(21.11) |
| |
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|