Problems : |
18.1 a)
|
Consider the two following planes that cut the crystallographic axes as indicated. Plane 1 cuts the axes at a / 3, b / 2 and c /4 and plane 2 cuts the axes at a / 2, b /3 and 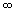 . What are the Miller indices of these planes ? . What are the Miller indices of these planes ? |
| |
|
18.1 b) |
Draw the planes for which the Miller indices are (112), (200), (120) and (221) |
| |
|
| 18.2 a)
|
In the Born-Haber cycle for the formation of a crystalline ionic solid, what are the parameters are there which need to be experimentally determined ? |
| |
|
| 18.2 b) |
Calculate the electron affinity of the F atom using the data given below. All energies are in kcal / mol. |
| |
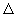 H diss ( F2 ) = 38, H diss ( F2 ) = 38, 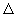 H f ( NaF ) = 136, H f ( NaF ) = 136, 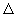 H vap [Na (s) ] = 24 H vap [Na (s) ] = 24 |
| |
I.E (Na) = 117.7 and UL ( NaF ) = 212.8 |
| |
|
| 18.3) |
The Born-Lande equation for the Lattice energy of ionic crystals is |
| |
UL = - NA M z, z2e2 ( 1-1 / n ) / r0 (in CGS units) |
| |
Where z1 e and -z2 e are the charges on the cation and the anion, NA = Avogadro number, M = Madelung constant, r0 = closest equilibrium distance between the anion and the cation and n = Born exponent. The value of n depends closed shell electronic configuration of the ion. The close shell configuration may resemble any of the rare gas atoms, He, Ne, Ar, Kr and Xe. The values of n for these configurations are 5, 7, 9, 10 and 11 respectively. If the value of n for the anion is n1 and that for cation is n2, then an average value of ( n1 + n2 ) / 2 may be taken for the Lattice. Using this formula and M = 1.747, determine the lattice energies for MgO ( r0 = 2.1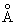 ) and NaCl ( r0 = 2.81 ) and NaCl ( r0 = 2.81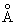 ) . How does this value for NaCl compare with the experimental value of UL ? ) . How does this value for NaCl compare with the experimental value of UL ? |
| |
|
| 18.4) |
What are the unit cells for the NaCl and the CsCl structures ? How many atoms are there in these unit cells ? |
| |
|
| 18.5) |
The edge length of the Ag FCC structure is 408.6 pm An X-ray beam produces a strong interference (intense reflection ) from the 111 planes at 2 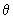 = 38.2 o . What is the X- ray wavelength ? = 38.2 o . What is the X- ray wavelength ? |
| |
|
| 18.6) |
The X - rays of wavelength 154.2 pm produce reflections from the 200 planes and the 111 plane of Cu which has FCC structure and density of 8.935 g /cm3 . At what angles will the diffracted intensity be maximum? |
| |
|
| 18.7) |
The molecular weight of NaCl is 58.448 and its density 2.165 g / cm3. What is the edge length of a cube that contains one mole of NaCl ? How many sodium and chloride ions lie along this edge if the distance between the nearest neighbour ions is 2.819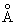 ? Calculate the Avogadro number using the information given above. ? Calculate the Avogadro number using the information given above. |
| |
|
| 18.8) |
From the face of a FCC lattice of NaCl, the Bragg diffraction from X-rays of 0.0586 nm wavelength occurs at an angle of 5o 58'. What is the distance separating these planes and what is the smallest distance between Na+ and Cl - and Cl - and Cl - ? Study the NaCl structure closely for a clear picture of the problem. |
| |
|
| 18.9) |
The atoms / ions in a crystal vibrate similar to a mass at the end of a string. For the mass at the end of a string, vibrational frequency increases with decreasing mass. It is found that the heat capacities of solids of lighter atoms such as Be, B and C are lower than the standard equipartion value of 6 cal /mol at room temperature. Can you make a connection between the heat capacity values and the dependence of frequency on mass? |
| |
|
| 18.10) |
The lattice parameter of the FCC silver unit cell is 408.6 pm. An X-ray beam produces a strong reflection from the 111 plane at angle 2 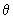 = 38.2o . What is the wavelength of the X-ray ? = 38.2o . What is the wavelength of the X-ray ? |
| |
|
| 18.11) |
X-rays with 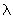 = 154.2 pm produce reflections from the 110 and 200 planes of FCC Cu of density 8.935 g / cm3. At what angles will these reflections appear? = 154.2 pm produce reflections from the 110 and 200 planes of FCC Cu of density 8.935 g / cm3. At what angles will these reflections appear? |
| |
|
| 18.12) |
X- rays of wavelength = 179 pm produce a reflection at 2 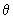 = 47.2o from the 110 planes of BCC lattice. Calculate the edgelength of the unit cell. = 47.2o from the 110 planes of BCC lattice. Calculate the edgelength of the unit cell. |
| |
|
| |