In Fig 18.4 the plane containing the atoms intersects the x axis at a. This plane does not intersect with the y and z axes at all. We may rephrase this by saying that the intersections with y and z axis at y =
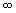 and z = and z =
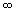 . The x, y and z intersections are at ( a, . The x, y and z intersections are at ( a,
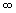 , ,
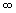 ). Taking the reciprocals of these, we get ( 1/a, 0, 0 ) and since a, b and c are characteristics of the crystal, we can simply refer to it as (100) ). Taking the reciprocals of these, we get ( 1/a, 0, 0 ) and since a, b and c are characteristics of the crystal, we can simply refer to it as (100) |
| These are the Miller indices of this plane. Using the same procedure verify that the Miller indices of the other planes in the figure (18.4) are (110), (111). In a simple cubic lattice, the (100) plane is identical to the (1/2, 0 0 )plane, because it has exactly the same density and the relative positions of atoms / ions. Therefore all planes parallel to the (100) planes may be referred to as the (100) planes. In a "body centered" cubic lattice such as the CsCl lattice, the (100) planes containing the Cl- ions would be different from the (200) planes
containing
the Cs+ ions. Now that we can label all these planes accurately, let us see how the distance between the planes can be determined using Bragg's law.
|