This is a simple and elegant law which is central to the analysis of diffraction data. This law relates the angle
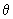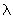( at which there is a maximum in diffracted intensity ) to the wavelength of X-rays and the inter-layer distance d between the planes of atoms / ions / molecules in the lattice. Figure 18.2 illustrates the details involved in the derivation of Bragg's Law.
Figure 18.2 Details involved in the derivation of Bragg's Law.
The layers of atoms are indicated by the labels to the right of the lines. The Lattice points are denoted by solid circles. The dashed lines along the row of atoms are only for guiding the eyes. The rays R1 and R2 are parallel and they have the same phase till they are at b and e respectively. The ray R2 traverses an additional distances efg. This additional distance causes a phase difference between rays R1 and R2. If rays R1 and R2 are at an angle of with respect to the atomic planes, then the angles e b f and f b g are also and the path length ef and fg are both equal to d sin where d is the perpendicular distance between any two adjacent layers. For constructive interference between rays R1 and R2, the path difference between R1 and R2 has to be an integral multiple of , the wavelength of X-rays used, i.e.,
2d sin = n ( Braggs Law )
(18.1)
The reflection of R2 is called a first order reflection as it is from the first inner layer. The ray R3 which is reflected by layer 3 is a second order reflection. The intensities of reflected light from the inner layers ( 3, 4 (not shown) and so on ) is much less and the major diffraction is brought out by the first inner layer. From the intense peaks of the diffraction patterns, the distances between various crystal planes can be determined. We now move on to the labeling of the lattice planes through Miller indices.
( at which there is a maximum in diffracted intensity ) to the wavelength 
of X-rays and the inter-layer distance d between the planes of atoms / ions / molecules in the lattice. Figure 18.2 illustrates the details involved in the derivation of Bragg's Law. 
