At equilibrium when r = r0, dUL / dr = 0 and we get |
C = Me2 r0 n-1 / n and
|
| |
| UL = - Me2 / r0 [1-1/n]. |
(16.6) |
The lattice energy UL is the energy for the process of forming the solid from the ions: |
| |
A+(g) + X - (g)
 AX(s); AX(s);
 H = UL. H = UL.
|
(16.7) |
This is not an easy quantity that can be determined experimentally. We shall now illustrate how to obtain UL through a thermodynamic cycle (known as the Born Haber cycle) in the case of the NaCl lattice. We start with the normal forms of atoms at room temperature Na(s) and Cl2(g), obtain their gaseous forms Na(g) and Cl(g), through vaporization [ Hv (Na)] and dissociation for Cl2] ionize the gaseous atoms and then condense the ions into the ionic lattice. These steps can be expressed as in equations (16.8) to (16.11). Hv (Na)] and dissociation for Cl2] ionize the gaseous atoms and then condense the ions into the ionic lattice. These steps can be expressed as in equations (16.8) to (16.11). |
| |
Na (s) +1/2 Cl2 (g)
 Na(g) + Cl (g); Na(g) + Cl (g);  H = H =  H v (Na) + 1 / 2 D (Cl2) H v (Na) + 1 / 2 D (Cl2) |
(16.8) |
| |
Na (g) + Cl (g)
 Na+ (g) + Cl - (g); Na+ (g) + Cl - (g);  H = I(Na) - A(Cl) H = I(Na) - A(Cl) |
(16.9) |
| |
Na+ (g) + Cl - (g)
 NaCl (s), NaCl (s),  H = UL H = UL |
(16.10) |
| The resultant of the above three steps is |
| |
Na(s) +1/2 Cl2 (g)
 NaCl(s); NaCl(s);  H = H = 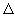 Hf (NaCl). Hf (NaCl). |
(16.11) |
| |
| Eq (16.11) gives the enthalpy of formation of NaCl. This is identical to the sum of equations (16.8), (16.9) and (16.10) by the first law of thermodynamics (energy and enthalpy changes are independent of path. Summing eq (16.8) to (16.10) we get |
| |
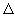 Hf (NaCl) = Hf (NaCl) = 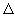 Hv (Na) +1/2 D (Cl2) + I (Na) - A (Cl)+ UL Hv (Na) +1/2 D (Cl2) + I (Na) - A (Cl)+ UL |
(16.12) |
| |
Here I is the ionization energy of Na ( Na
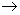 Na+ + e- ) and A (Cl) is the electron affinity of Cl - (i.e., the energy change for the process Cl - Na+ + e- ) and A (Cl) is the electron affinity of Cl - (i.e., the energy change for the process Cl -  Cl + e -. By taking all the quantities in kcal/mol units, we have, Cl + e -. By taking all the quantities in kcal/mol units, we have, |
| |
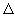 Hf (NaCl) = 24.14 +28.56 +118.4 - 83.4 + UL Hf (NaCl) = 24.14 +28.56 +118.4 - 83.4 + UL |
(16.13) |
| i) Lattice energy for an exponential repulsion form |
| ii) Calculations of UL |
| |
| Heat of formation of NaCl can be easily found from calorimetric measurements. A knowledge of this heat of formation allows us to calculate the lattice energy. We can also calculate the lattice energy by a knowledge of ionic sizes, the value of r0 and the value of the Madelung constant. If the calculated value of the lattice energy matches with the value calculated from the Born Haber cycle, it gives us an indication that the form of the interionic potentials and the sizes of ions that we have used are quite good. We thus have a method to test our theories of intermolecular forces with experimental results. |
| |