Figure 16.1 Unit cells. Sides are a, b and c and the angles are
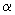 (between b and c in the bc plane), (between b and c in the bc plane),
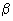 (in the ac plane, between a and c) and (in the ac plane, between a and c) and
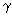 (between a and b in the ab plane. (a) cubic unit cell, (b) non-cubic unit cell (between a and b in the ab plane. (a) cubic unit cell, (b) non-cubic unit cell |
In a cubic crystal system (formed from cubic unit cells placed at the lattice points) there are four C3 axes placed in a tetrahedral arrangement. In Fig 16.1(a) the line joining the points 3 and 5, for example is a C3 axis. What this means is that if the unit cell/crystal is rotated by 120o, 240o and 360o (three angles, multiples of 120o), we get an arrangement which is indistinguishable from the original arrangement. Having only a C1 axis is as good as having no symmetry at all because every object has a C1 axis of symmetry, i.e., if you rotate it with respect to any axis by 360o, you will recover the original arrangement. A triclinic crystal has no symmetry or has only a C1 symmetry axis.
|