The dynamical variables (which characterize and describe the motion of an object) such as position, momentum, angular momentum and energy are replaced by “operators”. These operators operate on functions. When these operators operate on functions, new functions may result. However, in special cases, the result may be the original function multiplied by a constant. As an example, consider the operator d/dx ( the derivative operator) and functions sin(ax) and exp (ax). The result of operating the operator on the two functions is shown below. |
|
 |
(1.3) |
| |
 |
(1.4) |
| In the second example, we get a constant multiplied by the original function. The function exp (ax) is called an eigenfunction of the operator d/dx with an eigenvalue a. The function sin (ax) is not an eigenfunction of d/dx because on operating on the function by the operator d/dx, we do not get a constant multiplied by the same
function. An understanding of atomic and molecular structure and dynamics is based on the successful application of the following postulates.
|
| |
| 1) The dynamical variables are replaced by operators. e.g., |
| |
| a) Position x replaced by x. |
b) x-component of momentum px replaced by
 where i = where i = 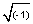 |
c) x component of kinetic energy px2 / 2m replaced by 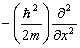 where m is the mass of the particle. where m is the mass of the particle. |
| |
| 2) Experimental observations on the dynamical variables yield the eigenvalues of the corresponding dynamical variables. When the energy of a system (atom, molecule or a cluster of molecules) is measured, the result will be an eigenvalue of the energy operator. |
| |
| 3) All the possible microscopic information of the system can be obtained from the wavefunction of the system which is a solution of the Schrödinger equation. |
 where H is the operator for the total energy of the system. The energy of the system is a sum of the kinetic energies of all the particles and the potential energy of interaction between all the particles. where H is the operator for the total energy of the system. The energy of the system is a sum of the kinetic energies of all the particles and the potential energy of interaction between all the particles. 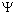 (which is called the wavefunction ) is a function of the coordinates of all the particles of the system. (which is called the wavefunction ) is a function of the coordinates of all the particles of the system. |
| |
4) The probability of finding a particle in a given volume element
(
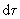 ) of space is given by ) of space is given by
 , where , where 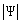 denotes the absolute value of denotes the absolute value of 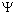 |
| |
| |