cladding. We hence should have
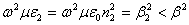 where where 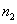 is the refractive index of the cladding. is the refractive index of the cladding.
Since 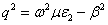 is negative, let us define a real quantity is negative, let us define a real quantity 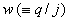 such that such that 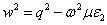 . .
Let us now look at the modified Bessel's functions, as shown in figures 6 & 7. For modified Bessel's functions of the 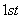 kind, as kind, as 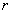 increases, that is, as we move away from the axis of the fiber the field monotonically increases and when increases, that is, as we move away from the axis of the fiber the field monotonically increases and when 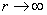 field goes to infinity. Since the energy source is inside the core, the fields cannot grow indefinitely away from the core. The only acceptable situation is that the field decays away from the core i.e., for larger values of field goes to infinity. Since the energy source is inside the core, the fields cannot grow indefinitely away from the core. The only acceptable situation is that the field decays away from the core i.e., for larger values of 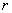 . This behavior is correctly given by the Modified Bessel function of second kind, . This behavior is correctly given by the Modified Bessel function of second kind, 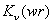 . .
So we conclude that the modified Bessel function of 1 st kind 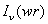 is not appropriate solution in the cladding. The correct solution would be only Modified Bessel function of 2 nd kind, is not appropriate solution in the cladding. The correct solution would be only Modified Bessel function of 2 nd kind, 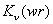 . . |