We can see from figure 4 that except 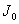 , all the other Bessel functions go to zero as the argument goes to zero. Only , all the other Bessel functions go to zero as the argument goes to zero. Only 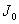 approaches approaches 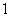 as its argument approaches zero. All Bessel functions have oscillatory behavior and their amplitude slowly decreases as the argument increases. as its argument approaches zero. All Bessel functions have oscillatory behavior and their amplitude slowly decreases as the argument increases.
Figure 5 shows the behavior of the Neumann function as a function of its argument,  . The important thing to note is, the Bessel functions . The important thing to note is, the Bessel functions 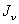 are finite for all values of the argument, whereas the Neumann functions are finite for all values of argument except zero. When the argument tends to zero, the Neumann functions tend to are finite for all values of the argument, whereas the Neumann functions are finite for all values of argument except zero. When the argument tends to zero, the Neumann functions tend to 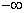 . .
|