• For incompressible flows, the Navier-Stokes equations can be rearranged in the form

(33.1a)

(33.1b)

(33.1c)

and

(33.2)

• Express the velocity components and pressure in terms of time-mean values and corresponding fluctuations. In continuity equation, this substitution and subsequent time averaging will lead to

or,

Since,

We can write

(33.3a)

From Eqs (33.3a) and (33.2), we obtain

(33.3b)

• It is evident that the time-averaged velocity components and the fluctuating velocity components, each satisfy the continuity equation for incompressible flow.
  
• Imagine a two-dimensional flow in which the turbulent components are independent of the z -direction. Eventually, Eq.(33.3b) tends to

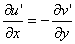  (33.4)

On the basis of condition (33.4), it is postulated that if at an instant there is an increase in u' in the x -direction, it will be followed by an increase in v' in the negative y -direction. In other words, 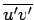is non-zero and negative. (see Figure 33.2)

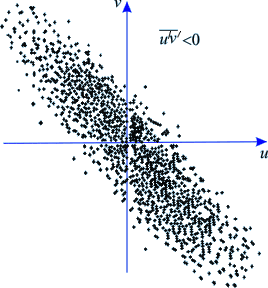
Fig 33.2 Each dot represents uν pair at an instant

• Invoking the concepts of eqn. (32.8) into the equations of motion eqn (33.1 a, b, c), we obtain expressions in terms of mean and fluctuating components. Now, forming time averages and considering the rules of averaging we discern the following. The terms which are linear, such as and vanish when they are averaged [from (32.6)]. The same is true for the mixed terms like , or , but the quadratic terms in the fluctuating components remain in the equations. After averaging, they form , etc.