Chapter 10 : Turbulent Flow

Lecture 33 :



Contd. from previous slide

  • If we perform the aforesaid exercise on the x-momentum equation, we obtain



 

using rules of time averages,

We obtain

                 

  • Introducing simplifications arising out of continuity Eq. (33.3a), we shall obtain.

                                                                                                                                                  
  • Performing a similar treatment on y and z momentum equations, finally we obtain the momentum equations in the form.

In x direction,

    

 (33.5a)

In y direction,

  

 (33.5b)

In z direction,

 

(33.5c)

  • Comments on the governing equation :

    1. The left hand side of Eqs (33.5a)-(33.5c) are essentially similar to the steady-state Navier-Stokes equations if the velocity components u, v and w are replaced by $ \bar{u}$, $ \bar{v}$ and .

    2. The same argument holds good for the first two terms on the right hand side of Eqs (33.5a)-(33.5c).

    3. However, the equations contain some additional terms which depend on turbulent fluctuations of the stream. These additional terms can be interpreted as components of a stress tensor.

  • Now, the resultant surface force per unit area due to these terms may be considered as

In x direction, 

        

(33.6a)

In y direction, 

 (33.6b)

In z direction, 

     

 (33.6c)

 

  • Comparing Eqs (33.5) and (33.6), we can write

           (33.7)

  • It can be said that the mean velocity components of turbulent flow satisfy the same Navier-Stokes equations of laminar flow. However, for the turbulent flow, the laminar stresses must be increased by additional stresses which are given by the stress tensor (33.7). These additional stresses are known as apparent stresses of turbulent flow or Reynolds stresses . Since turbulence is considered as eddying motion and the aforesaid additional stresses are added to the viscous stresses due to mean motion in order to explain the complete stress field, it is often said that the apparent stresses are caused by eddy viscosity . The total stresses are now

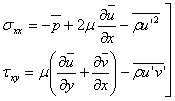
(33.8)

and so on. The apparent stresses are much larger than the viscous components, and the viscous stresses can even be dropped in many actual calculations .