|
Contd. from Previous slide
- However, the fluctuating components do not bring about the bulk displacement of a fluid element. The instantaneous displacement is
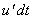 , and that is not responsible for the bulk motion. We can conclude from the above , and that is not responsible for the bulk motion. We can conclude from the above
Due to the interaction of fluctuating components, macroscopic momentum transport takes place. Therefore, interaction effect between two fluctuating components over a long period is non-zero and this can be expressed as
Taking time average of these two integrals and write
and
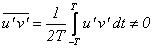 |
(32.4b) |
- Now, we can make a general statement with any two fluctuating parameters, say, with f ' and g' as
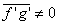 |
(32.5b) |
The time averages of the spatial gradients of the fluctuating components also follow the same laws, and they can be written as
- The intensity of turbulence or degree of turbulence in a flow is described by the relative magnitude of the root mean square value of the fluctuating components with respect to the time averaged main velocity. The mathematical expression is given by
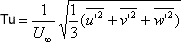 |
(32.7a) |
The degree of turbulence in a wind tunnel can be brought down by introducing screens of fine mesh at the bell mouth entry. In general, at a certain distance from the screens, the turbulence in a wind tunnel becomes isotropic, i.e. the mean oscillation in the three components are equal,
In this case, it is sufficient to consider the oscillation u' in the direction of flow and to put
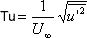 |
(32.7b) |
This simpler definition of turbulence intensity is often used in practice even in cases when turbulence is not isotropic.
Following Reynolds decomposition, it is suggested to separate the motion into a mean motion and a fluctuating or eddying motion. Denoting the time average of the 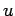 component of velocity by component of velocity by 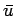 and fluctuating component as and fluctuating component as 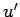 , we can write down the following, , we can write down the following,
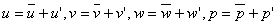
By definition, the time averages of all quantities describing fluctuations are equal to zero.
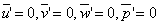 |
(32.8) |
The fluctuations u', v' , and w' influence the mean motion 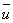 , , 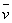 and and 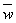 in such a way that the mean motion exhibits an apparent increase in the resistance to deformation. In other words, the effect of fluctuations is an apparent increase in viscosity or macroscopic momentum diffusivity . in such a way that the mean motion exhibits an apparent increase in the resistance to deformation. In other words, the effect of fluctuations is an apparent increase in viscosity or macroscopic momentum diffusivity .
- Rules of mean time - averages
If f and g are two dependent variables and if s denotes anyone of the independent variables x, y
End of Lecture 32!
To start next lecture click next button or select from left-hand-side.
|
|