|
Reynolds decomposition of turbulent flow :
- The Experiment: In 1883, O. Reynolds conducted experiments with pipe flow by feeding into the stream a thin thread of liquid dye. For low Reynolds numbers, the dye traced a straight line and did not disperse. With increasing velocity, the dye thread got mixed in all directions and the flowing fluid appeared to be uniformly colored in the downstream flow.
The Inference: It was conjectured that on the main motion in the direction of the pipe axis, there existed a superimposed motion all along the main motion at right angles to it. The superimposed motion causes exchange of momentum in transverse direction and the velocity distribution over the cross-section is more uniform than in laminar flow. This description of turbulent flow which consists of superimposed streaming and fluctuating (eddying) motion is well known as Reynolds decomposition of turbulent flow.
(ii) Space average for a homogeneous turbulence:
For a stationary and homogeneous turbulence, it is assumed that the two averages lead to the same result: 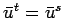 and the assumption is known as the ergodic hypothesis. and the assumption is known as the ergodic hypothesis.
- In our analysis, average of any quantity will be evaluated as a time average . Take a finite time interval t1. This interval must be larger than the time scale of turbulence. Needless to say that it must be small compared with the period t2 of any slow variation (such as periodicity of the mean flow) in the flow field that we do not consider to be chaotic or turbulent .
Thus, for a parallel flow, it can be written that the axial velocity component is
As such, the time mean component
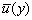 determines whether the turbulent motion is steady or not. The symbol determines whether the turbulent motion is steady or not. The symbol
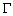 signifies any of the space variables. signifies any of the space variables.
- While the motion described by Fig.32.6(a) is for a turbulent flow with steady mean velocity the Fig.32.6(b) shows an example of turbulent flow with unsteady mean velocity. The time period of the high frequency fluctuating component is t1 whereas the time period for the unsteady mean motion is t2 and for obvious reason t2>>t1. Even if the bulk motion is parallel, the fluctuation u ' being random varies in all directions.
- The continuity equation, gives us
Invoking Eq.(32.1) in the above expression, we get
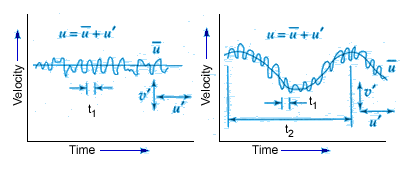
Fig 32.6 Steady and unsteady mean motions in a turbulent flow
Since 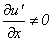 , Eq.(32.2) depicts that y and z components of velocity exist even for the parallel flow if the flow is turbulent. We have- , Eq.(32.2) depicts that y and z components of velocity exist even for the parallel flow if the flow is turbulent. We have-
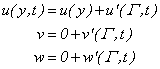 |
(32.3) |
|