|
...contd...Analysis of Potential Flows through Complex Variables
Let us combine a source and sink now. Refer to Figure 21.4. The complex potential is given by
| |
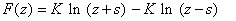 |
(22.24) |
This follows
| with |
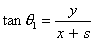 and and 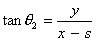 |
|
We know,
| or, |
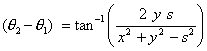 |
|
| Therefore, |
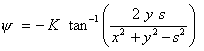 |
(22.25) |
| We also find |
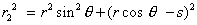 and and 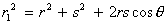 |
|
That results in
| |
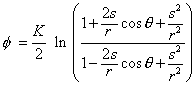 |
(22.26) |
Under the limiting condition of 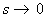 (the flow becomes a doublet) (the flow becomes a doublet)
We also know,
The strength of the doublets given by 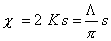
We get family of velocity potential from 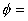 constant lines constant lines
| or, |
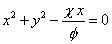 |
|
| or, |
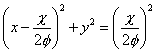 |
(22.27) |
This is the equation for 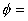 constant lines (also see Figure 21.5) constant lines (also see Figure 21.5)
Now from equation (22.25), for the limiting case of 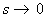 , one can write , one can write
| |
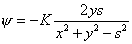 [as [as 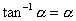 under the limiting case] under the limiting case] |
|
| or, |
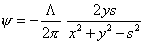 |
|
| or, |
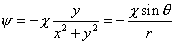 |
|
The streamlines associated with the doublet are
| |
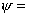 constant lines, which can be expressed as constant lines, which can be expressed as |
|
| or, |
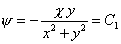 |
|
| or, |
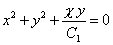 |
|
| or, |
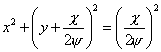 |
(22.28) |
This is the equation for 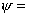 constant lines (see Figure 21.5) constant lines (see Figure 21.5)
Therefore for the doublet
| and, |
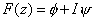 |
|
It can also be written as
| |
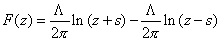 |
(22.30) |
If 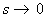 the the 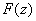 represents a doublet. represents a doublet.
Under the limiting conditions,
| |
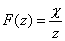
|
(22.31)
|
Thus, by using the elementary complex potential for source, sink, doublet, uniform flow, vortex flow etc more complicated fields can be constructed via the method of superposition. Especially, external flow past objects of various shapes can be simulated. However, for the first course, we shall follow simpler approach and construct various complex flows without using the route of complex potentials. We shall take up such exercises in the following lectures.
End of Lecture 22!
To start next lecture click next button or select from left-hand-side.
|
|