|
Streamlines, Velocity Potential for a Doublet
We have seen in the last lecture that the streamlines associated with the doublet are
If we replace sinθ by y/r, and the minus sign be absorbed in C1 , we get
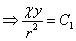 |
(21.17a) |
Putting 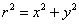 we get we get
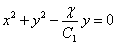 |
(21.17b) |
Equation (21.17b) represents a family of circles with
-
radius :
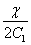
-
centre :
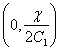
-
For x = 0, there are two values of y, one of them=0.
-
The centres of the circles fall on the y-axis.
-
On the circle, where y = 0, x has to be zero for all the values of the constant.
-
family of circles formed(due to different values of C1 ) is tangent to x-axis at the origin.
These streamlines are illustrated in Fig. 21.5.

Fig 21.5 Streamlines and Velocity Potential Lines for a Doublet
Due to the initial positions of the source and the sink in the development of the doublet , it is certain that
and
Velocity potential lines
In cartresian coordinate the equation becomes
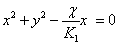 |
(21.18) |
Once again we shall obtain a family of circles
-
radius: 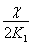
-
centre:
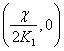
-
The centres will fall on x-axis.
-
For y = 0 there are two values of x, one of which is zero.
-
When x = 0, y has to be zero for all values of the constant.
-
These circles are tangent to y-axis at the origin.
In addition to the determination of the stream function and velocity potential, it is observed that for a doublet
As the centre of the doublet is approached; the radial velocity tends to be infinite.
It shows that the doublet flow has a singularity.
Since the circulation about a singular point of a source or a sink is zero for any strength, it is obvious that the circulation about the singular point in a doublet flow must be zero i.e. doublet flow  =0 =0
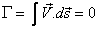 |
(21.19) |
Applying Stokes Theorem between the line integral and the area-integral
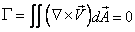 |
(21.20) |
From Eq. 21.20 the obvious conclusion is
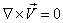 i.e., doublet flow is an irrotational flow. i.e., doublet flow is an irrotational flow.
End of Lecture 21!
To start next lecture click next button or select from left-hand-side.
|
|