|
Flow About a Cylinder without Circulation
-
Inviscid-incompressible flow about a cylinder
in uniform flow is equivalent to the superposition of a uniform flow and a doublet.
-
The doublet has its axis of development parallel to the direction of the uniform flow (x-axis in this case).
-
The potential and stream function for this flow will be the sum of those for uniform flow and doublet.
Potential Function
Stream function
Streamlines
In two dimensional flow, a streamline may be interpreted as
and
Hence, a streamline may also be considered as the contour of an impervious two-dimensional body .
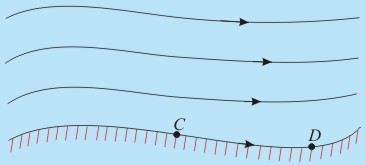
Fig 22.1 Surface Streamline
Figure 22.1 shows a set of streamlines.
The streamline C-D may be considered as the edge of a two-dimensional body .
-
other streamlines form the flow about the boundary.
In order to form a flow about the body of interest, a streamline has to be determined which encloses an area
whose shape is of practical importance in fluid flow. This streamline describes the boundary of a two-dimensional solid body. The remaining streamlines outside this solid region, constitute the flow about this body.
If we look for the streamline whose value is zero, we will obtain
|
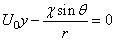 |
(22.1)
|
replacing y by rsinθ, we have
|
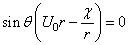 |
(22.2)
|
Solution of Eq. 22.2
-
If θ = 0 or θ = π, the equation is satisfied. This indicates that the x-axis is a part of the streamline
Ψ = 0.
-
When the quantity in the parentheses is zero, the equation is identically satisfied . Hence it follows that
|
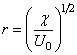 |
(22.3)
|
Interpretation of the solution
There is a circle of radius
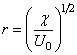 which is an intrinsic part of the streamline
Ψ = 0. which is an intrinsic part of the streamline
Ψ = 0.
This is shown in Fig.22.2
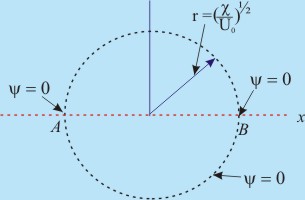
Fig 22.2 Streamline ψ = 0 in a Superimposed Flow of Doublet and Uniform Stream
Stagnation Points
Let us look at the points of intersection of the circle and x- axis , i.e. the points A and B in the above figure. The polar coordinate of these points are
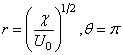 for point A for point A |
|
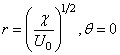 for point B for point B |
|
The velocity at these points are found out by taking partial derivatives of the velocity potential in two orthogonal directions and then substituting the proper values of the coordinates.
Since, 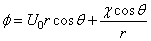 |
|
|
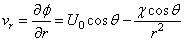 |
(22.4a)
|
|
At point A |
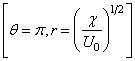
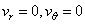
|
|
At point B |
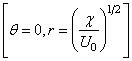
|
The points A and B are the stagnation points through which the flow divides and subsequently reunites forming a zone of circular bluff body.
The circular region, enclosed by part of the streamline ψ = 0 could be imagined as a solid cylinder in an inviscid flow. At a large distance from the cylinder the
flow is moving uniformly in a cross-flow configuration.
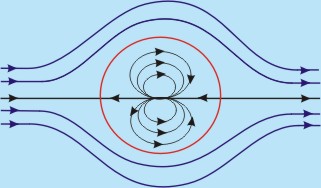
Fig. 22.3 Inviscid Flow past a Cylinder
Figure 22.3 shows the streamlines of the flow.
-
The streamlines outside the circle describe the flow pattern of the inviscid irrotational flow across a cylinder.
-
The streamlines inside the circle may be disregarded since this region is considered as a solid obstacle.
|