We can now form different flow patterns by superimposing the velocity potential and stream functions of the elementary flows stated above.
In order to develop a doublet, imagine a source and a sink of equal strength K at equal distance s from the origin along x-axis as shown in Fig. 21.4.
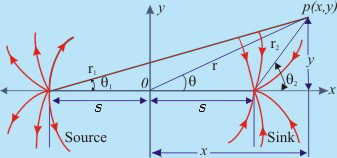
Fig 21.4 Superposition of a Source and a Sink
From any point p(x, y) in the field, r1 and r2 are drawn to the source and the sink. The polar coordinates of this point (r, θ) have been shown.
The potential functions of the two flows may be superimposed to describe the potential for the combined flow at P as
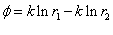 |
(21.11) |
Similarly,
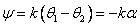 |
(21.12) |
where 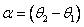 |
|
Expanding θ1 and θ2
in terms of coordinates of p and s
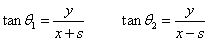 |
(21.13) |
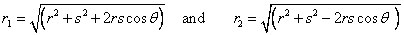 |
(21.14) |
Using
we find
 |
|
or, 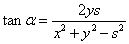 |
|
Hence the stream function and the velocity potential function are formed by combining Eqs (21.12) and (21.13), as well as Eqs(21.11) and (21.14) respectively
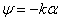 |
|
Hence 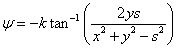 ------- Stream Function ------- Stream Function |
(21.15) |
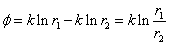 |
|
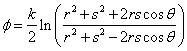 ----- Potential Function ----- Potential Function |
(21.16) |
Doublet is a special case when a source as well as a sink are brought together in such a way that
These are assumed to be accomplished in a manner which makes the product of s and
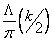 (in limiting case) a finite value c (in limiting case) a finite value c
This gives us
|