Dynamic Forces on Plane Surfaces due to the Impingement of Liquid Jets

Force on a stationary surface Consider a stationary flat plate and a liquid jet of cross sectional area ”a” striking with a velocity V at an angle θ to the plate as shown in Fig. 11.3a.

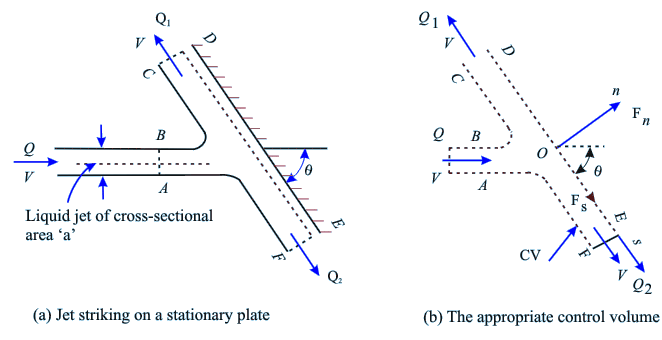
Fig 11.3 Impingement of liquid Jets on a Stationary Flat Plate

To calculate the force required to keep the plate stationary, a control volume ABCDEFA (Fig. 11.3a) is chosen so that the control surface DE coincides with the surface of the plate. The control volume is shown separately as a free body in Fig. 11.3b. Let the volume flow rate of the incoming jet be Q and be divided into Q₁ and Q₂ gliding along the surface (Fig. 11.3a) with the same velocity V since the pressure throughout is same as the atmospheric pressure, the plate is considered to be frictionless and the influence of a gravity is neglected (i.e. the elevation between sections CD and EF is negligible).

Coordinate axes are chosen as 0s and 0n along and perpendicular to the plate respectively. Neglecting the viscous forces. (the force along the plate to be zero),the momentum conservation of the control volume ABCDEFA in terms of s and n components can be written from Eq.(10.18d) as

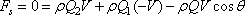(11.5a)

and

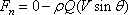(11.5b)

where F_s and F_n are the forces acting on the control volume along 0s and 0n respectively,

From continuity,         

With the help of Eqs (11.5a) and (11.6), we can write

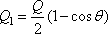	(11.7a)
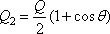	(11.7b)

The net force acting on the control volume due to the change in momentum of the jet by the plate is F_n along the direction "On” and is given by the Eq. (11.7b) as

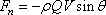(11.7c)

Hence, according to Newton’s third law, the force acting on the plate is

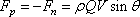(11.8)

If the cross-sectional area of the jet is ”a”, then the volume flow rate Q striking the plate can be written as Q = aV. Equation (11.8) then becomes

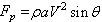(11.9)