|
Forces due to Flow Through Expanding
or Reducing Pipe Bends
Let
us consider, a fluid flow through an expander shown in Fig.
11.1a below. The expander is held in a vertical plane. The
inlet and outlet velocities are given by V1 and
V2 as shown in the figure. The inlet and outlet
pressures are also prescribed as p1 and p2.
The velocity and pressure at inlet and at outlet sections
are assumed to be uniform. The problem is usually posed for
the estimation of the force required at the expander support
to hold it in position.
Fig 11.1a Flow
of a fluid through an expander
For the solution of this
type of problem, a control volume is chosen to coincide with
the interior of the expander as shown in Fig. 11.1a. The control
volume being constituted by areas 1-2, 2-3, 3-4, and 4-1 is
shown separately in Fig.11.1b.
The external forces on
the fluid over areas 2-3 and 1-4 arise due to net efflux of
linear momentum through the interior surface of the expander.
Let these forces be Fx and Fy. Since
the control volume 1234 is stationary and at a steady state,
we apply Eq.(10.18d) and have for x and y components
| |
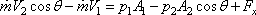
|
(11.1a) |
| and |
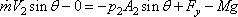
|
(11.1b) |
| or, |
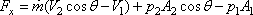 |
(11.2a) |
| and |
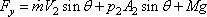 |
(11.2b) |
where 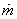 = mass
flow rate through the expander. Analytically it can be expressed
as = mass
flow rate through the expander. Analytically it can be expressed
as
where A1 and A2
are the cross-sectional areas at inlet and outlet of the expander
and the flow is considered to be incompressible.
M represents the mass of fluid contained in the expander at
any instant and can be expressed as
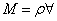 where where 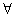 is the internal volume of the expander. is the internal volume of the expander. |
|
Thus, the forces Fx
and Fy acting on the control volume (Fig. 11.1b)
are exerted by the expander. According to Newton’s third
law, the expander will experience the forces Rx (= − Fx) and Ry ( = − Fy)
in the x and y directions respectively as shown in the free
body diagram of the expander. in fig 11.1c.
| Fig 11.1b Control
Volume Comprising the fluid contained in the expander
at any instant |
Fig
11.1c Free Body Diagram of the Expander
|
The expander will also experience
the atmospheric pressure force on its outer surface.
This is shown separately in Fig.
11.2.
Fig 11.2 Effect
of atmospheric pressure on the expander
From Fig.11.2 the net x and
y components of the atmospheric pressure force on the expander
can be written as
The
net force on the expander is therefore,
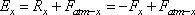 |
(11.3a) |
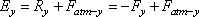 |
(11.3b) |
or,
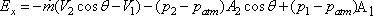 |
(11.4a) |
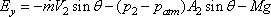 |
(11.4b) |
Note:
At this stage that if Fx and Fy are
calculated from the Eqs (11.2a) and (11.2b) with p1
and p2 as the gauge pressures instead of the absolute
ones the net forces on the expander Ex and Ey
will respectively be equal to −Fx and −Fy.
|