|
Force on a moving surface
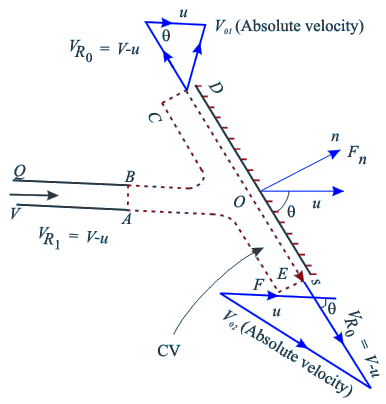
Fig 11.5 Impingement
of liquid jet on a moving flat plate
If the plate in the
above problem moves with a uniform velocity u in the direction
of jet velocity V (Fig. 11.5). The volume of the liquid striking
the plate per unit time will be
Physically, when the plate
recedes away from the jet it receives a less quantity of liquid
per unit time than the actual mass flow rate of liquid
delivered, say by any nozzle. When u = V, Q = 0 and when u
> V, Q becomes negative. This implies physically that when
the plate moves away from the jet with a velocity being equal
to or greater than that of the jet, the jet can never strike
the plate.
The control volume ABCDEFA
in the case has to move with the velocity u of the plate.
Therefore we have to apply Eq. (10.18d) to calculate the forces
acting on the control volume. Hence the velocities relative
to the control volume will come into picture. The velocity
of jet relative to the control volume at its inlet becomes
VR1 = V − u
Since the pressure remains
same throughout, the magnitudes of the relative velocities
of liquid at outlets become equal to that at inlet, provided
the friction between the plate and the liquid is neglected.
Moreover, for a smooth shockless flow, the liquid has to glide
along the plate and hence the direction of VR0,
the relative velocity of the liquid at the outlets, will be
along the plate. The absolute velocities
of the liquid at the outlets can be found out by adding vectorially
the plate velocity u and the relative velocity of the jet
V - u with respect to the plate. This is shown by the
velocity triangles at the outlets (Fig. 11.5). Coordinate
axes fixed to the control volume ABCDEFA are chosen as ”0s”
and ”0n” along and perpendicular to the plate
respectively.
The force acting
on the control volume along the direction ”0s”
will be zero for a frictionless flow. The net force acting
on the control volume will be along ”0n”
only. To calculate this force
Fn, the momentum theorem with respect to the control
volume ABCDEFA can be written as
Substituting Q from Eq (11.10),
Hence the force acting
on the plate becomes
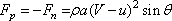 |
(11.11) |
If the plate moves with
a velocity u in a direction opposite to that of V (plate moving
towards the jet), the volume of liquid striking the plate
per unit time will be Q = a(V + u) and, finally, the
force acting on the plate would be
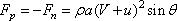 |
(11.12) |
From the comparison of the
Eq. (11.9) with Eqs (11.11) and (11.12), conclusion can be
drawn that for a given value of jet velocity V, the force
exerted on a moving plate by the jet is either greater or
lower than that exerted on a stationary plate depending upon
whether the plate moves towards the jet or-away from it respectively.
The power developed due to the motion of the plate can be
written (in case of the plate moving in the same direction
as that of the jet) as
| P = Fp . U |
|
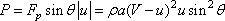 |
(11.13) |
|