Dynamic Forces on Curve Surfaces due to the Impingement of Liquid Jets

The principle of fluid machines is based on the utilization of useful work due to the force exerted by a fluid jet striking and moving over a series of curved vanes in the periphery of a wheel rotating about its axis. The force analysis on a moving curved vane is understood clearly from the study of the inlet and outlet velocity triangles as shown in Fig. 11.6.

The fluid jet with an absolute velocity V₁ strikes the blade at the inlet. The relative velocity of the jet V_r1 at the inlet is obtained by subtracting vectorially the velocity u of the vane from V₁. The jet strikes the blade without shock if β₁ (Fig. 11.6) coincides with the inlet angle at the tip of the blade. If friction is neglected and pressure remains constant, then the relative velocity at the outlet is equal to that at the inlet  (V_r2 = V_r1).

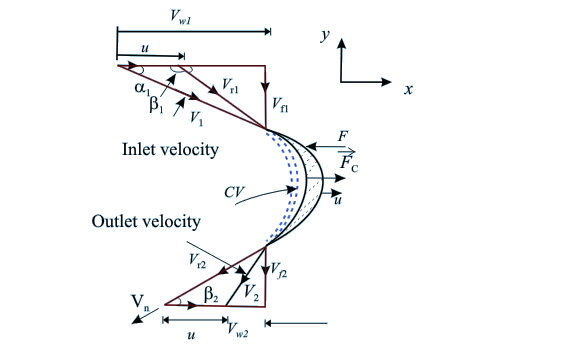
Fig  11.6    Flow of Fluid along a Moving Curved Plane

The control volume as shown in Fig. 11.6 is moving with a uniform velocity u of the vane.Therefore we have to use Eq.(10.18d) as the momentum theorem of the control volume at its steady state. Let F_c be the force applied on the control volume by the vane.Therefore we can write

To keep the vane translating at uniform velocity, u in the direction as shown. the force F has to act opposite to F_c Therefore,

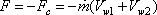(11.14)

From the outlet velocity triangle, it can be written

or,
or,
or,		(11.15a)

Similarly from the inlet velocity triangle. it is possible to write

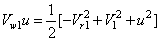(11.15b)

Addition of Eqs (11.15a) and (11.15b) gives

Power developed is given by

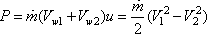(11.16)

The efficiency of the vane in developing power is given by

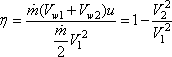(11.17)